• 1. 概述
• 2. 核心模块
  • 2.1 抑制增益和时频掩模
    • 2.1.1 谱减法
    • 2.1.2 维纳滤波
    • 2.1.3 统计信号方法
    • 2.1.4 理想二值掩模
  • 2.2 话音激活检测和语音存在概率
  • 2.3 噪声估计
    • 2.3.1 最小值跟踪算法
    • 2.3.2 直方图噪声估计算法
    • 2.3.3 递归平均噪声算法
    • 2.3.4 基于语音概率的递归平均算法
    • 2.3.5 最小值控制的递归平均（MCRA）算法
  • 2.4 SNR估计

1. 概述

单通道语音增强是语音信号处理中广泛研究的课题，主要作为前端去噪模块应用在提升音质、语音通信、辅助听觉、语音识别等领域。 单通道语音增强问题定义主要包括两个方面：

1. 输入信号是只有一路通道的带噪语音信号。

2. 处理目标是增强语音，降低噪声，也相当于分离“语音”与“非语音”信号。

不包括：

1. 多通道语音信号处理， 那属于阵列信号处理的范畴。

2. 区分/分离混合的不同人的语音（也就是鸡尾酒会问题），那属于盲源分离的范畴。

单通道语音增强传统的方法是滤波和统计信号处理，比如WebRTC的噪声抑制模块就是用维纳滤波。 这些传统的方法基本都在 《语音增强–理论与实践》一书中有详细讲解。

近几年机器学习方法兴起，也逐渐成为语音增强的主要研究方向，各种新型神经网络的方法都被尝试用在语音增强领域。这些新方法主要看近几年的InterSpeech会议、ICASSP会议和IEEE的期刊。

下面先对单通道语音增强号的基本处理步骤做个简单介绍。

假设麦克风采集到的带噪语音序列为$y[n]$，并且噪声都是加性噪声。则带噪语音序列为无噪语音序列与噪声序列的和。 原始语音信号与噪声均可视为随机信号。

$$y[n] = x[n] + d[n]$$

语音信号的处理一般都在频域，需要对带噪信号$y[n]$进行分帧、加窗、短时傅里叶变换（STFT）后，得到每一帧的频域信号，其中X，Y，D分别是干净语音、带噪信号和噪声的频域信号。

$$Y(\omega_{k}) = X(\omega_{k}) + D(\omega_{k})$$

语音增强的目标是对实际信号$X(\omega_{k})$的幅度和相位进行估计。但是因为相位不易估计、而且研究表明相位对去噪效果影响比较小\cite{wang1982unimportance}，所以大部分方法都只对幅度谱进行增强，而相位则沿用带噪信号的相位。

换句话说，语音增强就是要找出一个频域的实函数$H_{\omega_{k}}$, 并且将这个函数与带噪信号相乘，得到干净语音的估计。这个实函数称作抑制增益(Suppression Gain)。

$$\hat{X}(\omega_{k}) = H(\omega_{k})|Y(\omega_{k})|e^{j\theta_{y}(k)}$$

下面是单通道语音增强系统主要步骤的示意图，系统目标就是估计抑制增益，而抑制增益依赖于两个核心步骤：语音检测VAD和噪声估计模块。只有准确估计噪声谱$D(\omega_{k})$，才有可能准确估计抑制增益。 详细的VAD和噪声估计方法不在这篇文章里面详述，具体可以看参考文献。 一种简单的想法是先估计出VAD，如过判断此帧没有语音，则更新噪声谱，否则就沿用上一帧的噪声谱。

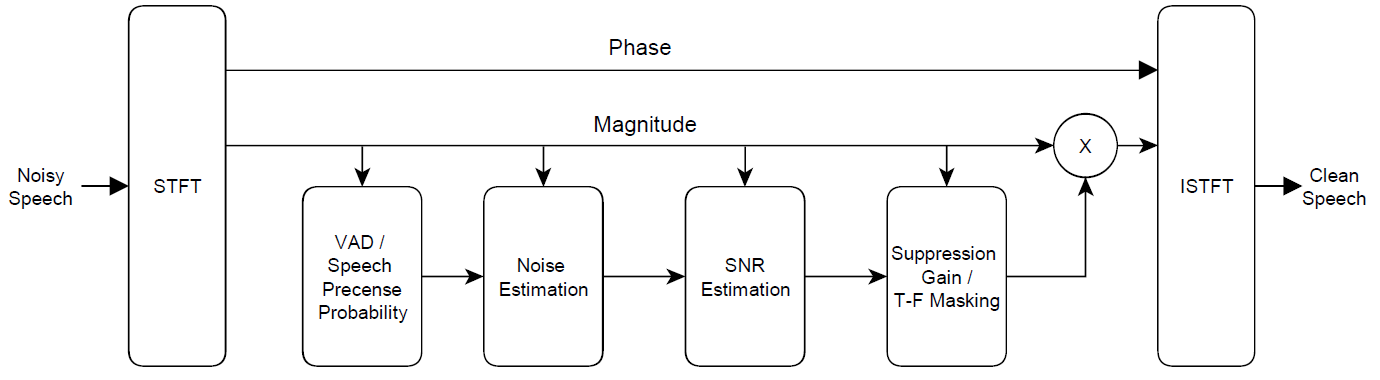
综上，语音增强的典型流程就是： 1 对带噪语音y[n]分帧， 每一帧进行DFT得到$Y(\omega_{k})$。 2 利用$Y(\omega_{k})$进行VAD检测和噪声估计。 3 计算抑制增益$H_{k}$。 4 抑制增益$H_{k}$与带噪信号谱相乘，得到纯净语音谱$\hat{X}(\omega_{k})$ 5 对$\hat{X}(\omega_{k})$进行IDFT,得到纯净语音序列的估计$x[n]$。

噪声估计模块可以估计噪声功率，也可以估计信噪比，避免信号幅度变化带来的误差。 定义后验信噪比：

$$\gamma_k = \frac{P_{yy}}{P_{dd}}$$

定义先验信噪比：

$$\xi_k = \frac{P_{xx}}{P_{dd}}$$

2. 核心模块

2.1 抑制增益和时频掩模

2.1.1 谱减法

谱减法是最直观的去噪声思想，就是带噪信号减去噪声的频谱，就等于干净信号的频谱。估计信号频谱的表达式如下，其中$\hat{D}(\omega_{k})$应是噪声估计模块得到的噪声频谱。

假设语音信号与噪声不相关，于是得到估计的信号功率谱是测量信号功率谱减去估计的噪声功率谱。

$$|X(\omega_{k})|^2 = |Y(\omega_{k})|^2 - |D(\omega_{k})|^2 P_{xx}(\omega_{k}) = P_{yy}(\omega_{k}) - P_{dd}(\omega_{k})$$

因此抑制增益函数即为：

$$H(\omega_{k}) = \sqrt{\frac{P_{yy}(\omega_{k}) - P_{dd}(\omega_{k})}{P_{yy}(\omega_{k})}} = \sqrt{\frac{\xi_k}{\xi_k+1}}$$

2.1.2 维纳滤波

维纳滤波的思想也很直接，就是将带噪信号经过线性滤波器变换来逼近原信号，并求均方误差最小时的线性滤波器参数。维纳滤波语音增强的目标就是寻找系数为实数的线性滤波器，使得滤波偶信号与原干净语音信号之间的均方误差最小。这是一个优化问题，目标是求使得均方误差最小的参数$H$

$$H(\omega_{k}) =\mathop{\arg\min}_{H(\omega_{k})} E\left[\left[X(\omega_{k}) - H(\omega_{k})Y(\omega_{k})\right]\left[X(\omega_{k}) - H(\omega_{k})Y(\omega_{k})\right]^*\right]$$

Gain用先验信噪比表示

$$H(\omega_{k}) = \frac{P_{xx}}{P_{yy}} = \frac{P_{xx}}{P_{xx} +P_{dd} } = \frac{\xi_k}{\xi_k + 1 }$$

2.1.3 统计信号方法

见博文《单通道语音增强之统计信号模型》。

2.1.4 理想二值掩模

待补充。

2.2 话音激活检测和语音存在概率

话音激活检测(Voice Activity Detection, VAD) 将语音帧二分为“纯噪声”和“语音噪声混合”两类。 说话人静音、停顿都会出现多帧的纯噪声，对这些帧无需估计语音信号，而可以用来估计噪声功率。 语音帧经过VAD分类后，进行不同的处理:

$H_0$：不含语音帧，更新噪声功率估计和Gain, 进行抑制；

$H_1$：包含语音帧，沿用上一帧的噪声功率和Gain，进行抑制。

语音存在概率SPP(Speech Presence Probability，SPP) 跟VAD作二分类不同，利用统计模型对每一帧估计出一个取值在[0,1]的语音存在概率，也就是一种soft-VAD。 SPP通常跟统计信号模型结合起来估计最终的Gain。

一种估计SPP的方法是根据测量信号$Y(\omega_{k})$估计每个频点的语音存在的后验概率，也就是 $P(H_1^k|Y(\omega_{k}))$。

根据贝叶斯公式：

$$P(H_1^k|Y(\omega_{k})) = \frac{P(Y(\omega_{k})|H_1^k)P(H_1)}{P(Y(\omega_{k})|H_1^k)P(H_1)+P(Y(\omega_{k})|H_0^k)P(H_0)}$$

定义语音不存在的先验概率$P(H_0^k)$为$q_k$, 语音存在的先验概率$P(H_1^k)$为$1-q_k$。假设噪声与语音信号为零均值复高斯分布。最终可以得到SPP计算公式：

$$P(H_1^k|Y(\omega_{k})) = \frac{1-q_k}{1-q_k+q_k(1+\xi_k')\exp(-\nu_k')}$$

其中为$\xi_k’$为条件信噪比，有$\xi_k’=\frac{\xi_k}{1-q_k}$ 及 $\nu_k’=\frac{\xi_k’}{\xi_k’+1}\gamma_k$。

语音不存在的先验概率$q_k$可以采用经验值，如0.5，或者进行累加平均， 也可以参考《语音增强—理论与实践》中更复杂的算法。

2.3 噪声估计

2.3.1 最小值跟踪算法

最小值跟踪发的思想是，噪声能量比较平稳， 带语音的片段能量总是大于纯噪声段。 对于每个频点，跟踪一段时间内最低的功率，那就是纯噪声的功率。

为了使功率估计更稳定，通常要对功率谱进行平滑处理：

$$P(\lambda, k) = \alpha P(\lambda-1,k) + (1-\alpha)|Y(\lambda, k)|^2$$

然后寻找当前第$\lambda$帧的最低功率$P_{min}$。简单的方法是直接比较前$D$帧的功率，得到最小值，计算速度较慢。 还有一种方法是对$P_{min}$进行非线性平滑，公式如下。

$$\begin{aligned} \text{if } &P_{min}(\lambda-1, k) < P(\lambda, k) \\ &P_{min}=\gamma P_{min}(\lambda-1, k) + \frac{1-\gamma}{1-\beta}\left[P(\lambda, k)-\beta P(\lambda-1, k)\right]\\ \text{else}&\\ &P_{min}=\gamma P_{min}(\lambda-1, k)\\ \text{end}& \end{aligned}$$

参数需要调优，可以参考文献中提供的取值：$\alpha=0.7$、$\beta=0.96$、$\gamma=0.998$。

2.3.2 直方图噪声估计算法

这种估计方法的思路是，噪声的能量变化比语音稳定，因此按频点统计一段时间内的能量直方图，每个频点出现频次最高的能量值就是噪声的能量。 主要包括以下几个步骤：

1.计算当前帧的功率谱 $|Y(\lambda, k)^2|$

2.计算当前帧前连续D帧功率谱密度直方图，选择每个频点k的频次最高的功率值$H_{max}(\lambda, k)$

3.滑动平均，更新噪声功率谱密度 $\hat{\sigma}_d^2(\lambda, k) = \alpha_m\hat{\sigma}_d^2(\lambda-1, k) + (1-\alpha_m)H_{max}(\lambda, k)$

2.3.3 递归平均噪声算法

当前帧的SNR很低，或者语音出现概率很低时，意味着当前信号功率很接近噪声功率，我们可以用当前帧的功率谱与前一帧估计的噪声功率进行加权平均，从而更新噪声功率谱。这就是递归平均法，通用的公式是：

$$\hat{\sigma}_d^2(\lambda, k) = \alpha(\lambda, k)\hat{\sigma}_d^2(\lambda-1, k) + \left[1-\alpha(\lambda,k)\right]|Y(\lambda, k)|^2$$

算法的核心变成了计算参数$\alpha(\lambda, k)$，研究者提出了不同的方法，比如可以根据后验信噪比$\gamma_k(\lambda)$计算参数：

$$\alpha(\lambda, k)=1-\text{min}\left\{1, \frac{1}{\gamma_k^p(\lambda)}\right\}$$

2.3.4 基于语音概率的递归平均算法

用$H_1^k$和$H_0^k$分别代表当前帧包含语音和不包含语音，从概率论的角度，当前帧的噪声功率期望值为：

$$\begin{aligned} \hat{\sigma}_d^2(\lambda, k) &= E\left[\sigma_d^2(\lambda, k)|Y(\lambda, k)\right] \\ &= E\left[\sigma_d^2(\lambda, k)|H_0^k\right]P(H_0^k|Y(\lambda, k)) + E\left[\sigma_d^2(\lambda, k)|H_1^k\right]P(H_1^k|Y(\lambda, k)) \end{aligned}$$

其中，当前帧不存在语音时，噪声功率就是信号功率，所以 $E\left[\sigma_d^2(\lambda, k)|H_0^k\right]= |Y(\lambda, k)|^2$。当前帧存在语音时，可以用前一帧估计的噪声功率来近似, $E\left[\sigma_d^2(\lambda, k)|H_1^k\right]=\hat{\sigma}_d^2(\lambda-1, k)$。噪声的递归平均算法转化为求当前帧每个频点的语音存在/不存在概率问题：

$$\hat{\sigma}_d^2(\lambda, k) = |Y(\lambda, k)|^2P(H_0^k|Y(\lambda, k)) + \hat{\sigma}_d^2(\lambda-1, k)P(H_1^k|Y(\lambda, k))$$

比照递归平均的通用公式，也就是 $\alpha(\lambda, k) =P(H_1^k|Y(\lambda, k))$。 使用前一节介绍的语音存在概率SPP计算方法求 $P(H_1^k|Y(\lambda, k))$即可。

2.3.5 最小值控制的递归平均（MCRA）算法

MCRA是一种将最小值跟踪与基于语音概率的递归平均结合起来的算法,核心思想是用当前帧功率谱平滑后与局部最小功率谱密度之比来估计语音概率。

$$S_r(\lambda, k) = \frac{S(\lambda, k)}{S_{min}(\lambda, k)}$$

以某阈值$\delta$对语音概率$p(\lambda, k)$进行二元估计

$$p(\lambda, k) = \left(S_r(\lambda, k)>\delta\right)?1:0$$

语音概率也可以进行平滑：

$$\hat{p}(\lambda, k) = \alpha_p\hat{p}(\lambda-1, k) + (1-\alpha_p)p(\lambda, k)$$

另外，如果将语音不存在是的噪声估计也做滑动平均，也就是

$\hat{\sigma}_d^2(\lambda, k) = \alpha\hat{\sigma}_d^2(\lambda-1, k)+(1-\alpha)|Y(\lambda, k)|^2$ 可以得到最终的噪声概率估计公式：

$$\hat{\sigma}_d^2(\lambda, k) = \alpha_d(\lambda, k)\hat{\sigma}_d^2(\lambda-1, k) + \left[1-\alpha_d(\lambda,k)\right]|Y(\lambda, k)|^2$$ $$\alpha_d(\lambda, k) = \alpha + (1-\alpha)\hat{p}(\lambda, k)$$

2.4 SNR估计

后验信噪比的估计比较直接，就是带噪信号功率与估计噪声功率之比： $\sigma_k^2$。然后$\gamma_k = Y_k^2/\sigma_k^2$。

先验信噪比是纯净信号功率与噪声功率之比，无法直接得知，需要更进一步估计。一种方法是简单谱减法，从功率角度$X_k^2= Y_k^2- \sigma_k^2$。 因此

$$\xi_k = \gamma_k - 1$$

更精确的方法是判决引导法（Decision-directed approach）， 滑动平均

$$\xi_k = aX_{k-1}^2/\sigma_k^2+(1-a)\text{max}(\gamma_k - 1, 0)$$

参考文献

[1] P. C. Loizou, Speech enhancement: theory and practice. CRC press, 2007.