wjchen

Never lose a holy curiosity.

C++实现离散傅里叶变换

11 Dec 2024 » 信号处理


DFT是离散傅里叶变换，是一种适合计算机实现的傅里叶变换形式。这个仓库的目标是学习如何实现DFT，并逐步优化。在开始学习怎么使用代码实现DFT之前，我们需要快速理解傅里叶变换和离散傅里叶变换的背景知识。

什么是傅里叶变换?

对物理世界的信号进行观察、测量，最直接的方式，是记录信号随着时间的变化。这就得到时域信号x(t)，表示时间方向的信号幅度。对信号进行时域分析，有很多数学工具。但是信号的一些特征，可能是非时变的、在时域上并不能直接感知的，数学家/物理学家会将信号转到某种变换域上去分析。

比如，在一场音乐会上录制的音频，有男低音的歌声、女高音的歌声、各种乐器或高或低的演奏声。音频信号在时域上，看起来像是杂乱无章变化的序列，只能看到有时候音量高，有时候音量低。我们如何分辨里面哪些声音是男低音、哪些是女高音、哪些是乐器、各自表演的歌曲是什么？


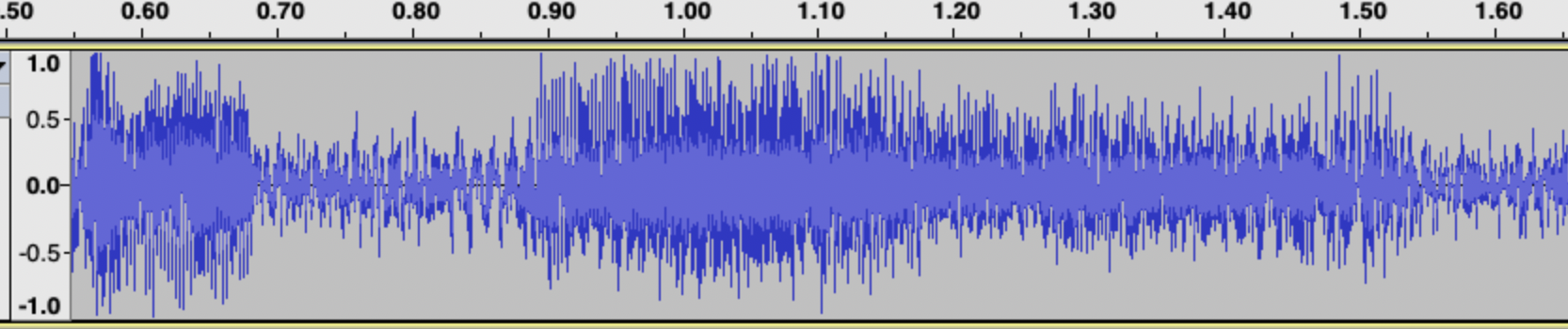
我们知道，声波是一种振动，其特征就是两个量：振动频率和振动幅度。振动频率越高的声音，人耳的感受更尖锐，振动频率越低，人耳感受越低沉。成人男性的声带一般较女性的声带更粗更宽，声带震动慢，因此一般男声更低沉、女声更高亢。而不同的乐器有不同的共振频率和谐波，比如琴弦越短，声音越高。如果我们把音乐的声波信号包含了哪些振动频率找出来，我们就能分析这首音乐包含了哪些乐器和演唱者、是在演奏什么歌曲了。如下图，这首音乐的频谱上看到不同的高亮频点，那就是该时刻演奏的频率特征。


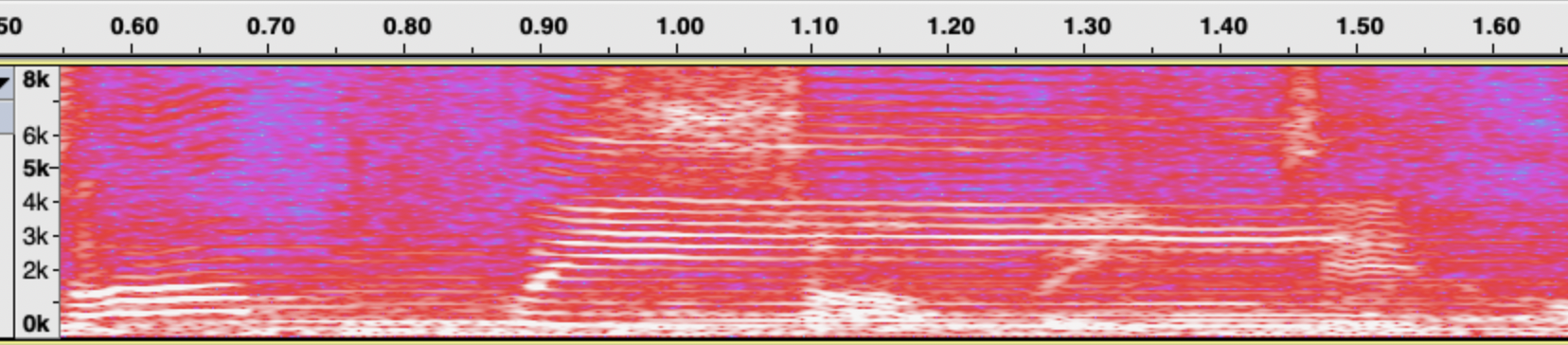
傅里叶变换就是这样一种数学工具，可以将时域信号中的（幅度，时间）变换到频域中的（幅度，频率）进行频率分析和处理。

这个变换是怎么实现的呢？我们回头看上面的音乐信号，将其中一段放大，可以看到一些相似波形在重复出现，而大波形里又叠加了一些小波形。看起来杂乱无章变化的时域序列，并不是真的杂乱无章，其实可以分解为不同周期信号的叠加。周期越长，就是频率越低，周期越短，就是频率越高。


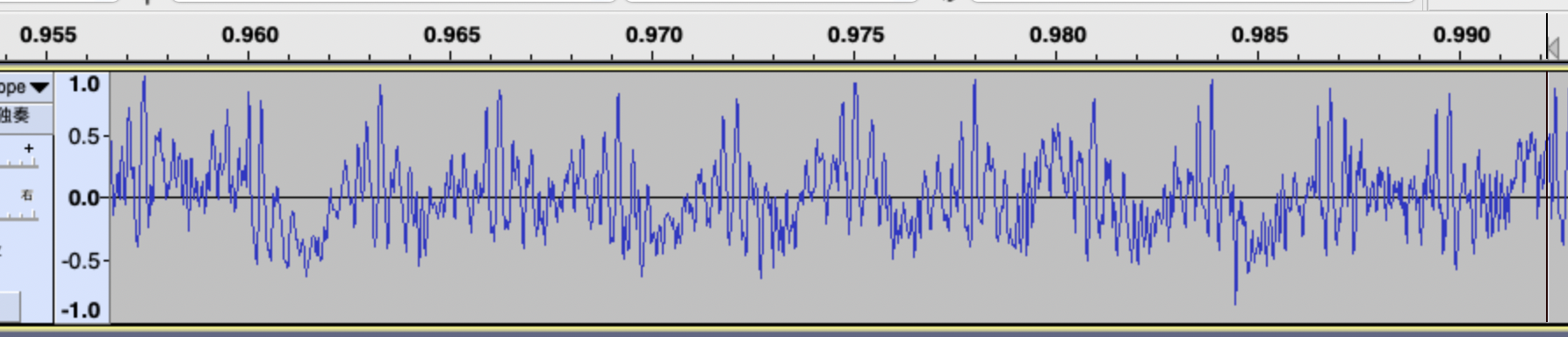
将一个时域信号，分解为不同频率的周期信号的线性叠加，这就是傅里叶变换的基础出发点。

傅里叶级数FS

傅里叶级数提供了一种数学表达，将一个周期函数分解成无限个三角函数sine和cosine的线性叠加。以下图为例，一个矩形波，可以分解成一个大的正弦波再叠加一系列小的正弦波。

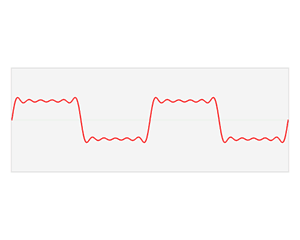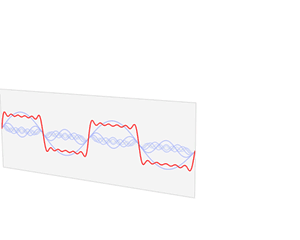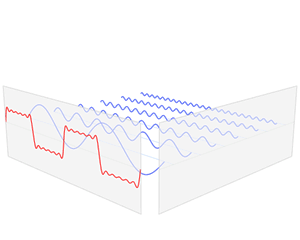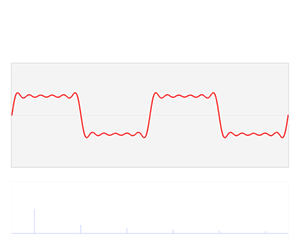
Fourier transform time and frequency domains (small).gif, CC0, By Lucas Vieira

傅里叶级数将一组倍频的三角函数作为正交基，周期信号可变换为这组正交基的权重。

实数形式傅里叶级数如下，其中 $T_0$ 是时域周期，$f_0 = 1/T_0$。：

\[\begin{aligned} f(t) & = \frac{a_0}{2}+\sum_{n=0}^{\infty} \left[a_n\cos(2\pi nf_0t)+b_n\sin(2\pi nf_0t)\right] \\ 其中 \\ a_0 & = \frac{1}{T_0}\int_{-T/2}^{T/2} f(t)dt \\ a_n & = \frac{2}{T_0}\int_{-T/2}^{T/2} f(t)\cos(2\pi nf_0t)dt \\ b_n & = \frac{2}{T_0}\int_{-T/2}^{T/2} f(t)\sin(2\pi nf_0t)dt \\ \end{aligned}\]

复数形式的傅里叶级数形式如下:

\[\begin{aligned} X(kf_0) & = \frac{1}{T_0}\int_{T0} x(t) e^{-j2\pi kf_0t}dt \\ x(t) & = \sum_{k=-\infty}^{\infty} X(kf_0)e^{j2\pi kf_0t} \end{aligned}\]

连续时间傅里叶变换CTFT

对于非周期信号，不能直接用傅里叶级数，但可认为这是一种特殊的周期函数，其周期趋近于无穷。这个条件下，傅里叶级数可以推导为傅里叶积分，得到的是一个频谱密度函数。

\[\begin{aligned} X(f) & = \lim_{T_0->\infty} \frac{1}{T_0}\int_{T0} x(t) e^{-j2\pi kf_0t}dt \end{aligned}\]

傅里叶积分可用来分析非周期连续信号的频谱密度，也可以用频谱密度恢复时域信号。这就是连续时间傅里叶变换CTFT。

\[\begin{aligned} X(f) & = \int_{t=-\infty}^{\infty} x(t) e^{-j2\pi ft}dt \\ x(t) & = \int_{k=-\infty}^{\infty} X(f)e^{j2\pi ft}df \end{aligned}\]

什么是DFT?

针对物理世界的连续信号，我们有连续时间傅里叶变换作为数学工具。但是电子计算机使用二进制器件进行计算、且只有固定的内存空间，故只能处理数字化的信号，也就是有限长的、离散化的、量化的信号。

而离散傅里叶变换（DFT）就是为数字世界设计的，一种时域信号离散且有限长、频域信号离散且有限长的变换。

时域离散化：离散时间傅里叶变换DTFT

首先，我们对连续信号时域上作离散化，按 $T_s$ 周期采样, 也就是将原信号乘以一个冲击串函数: $x(t)\delta(t-nT_s)$。

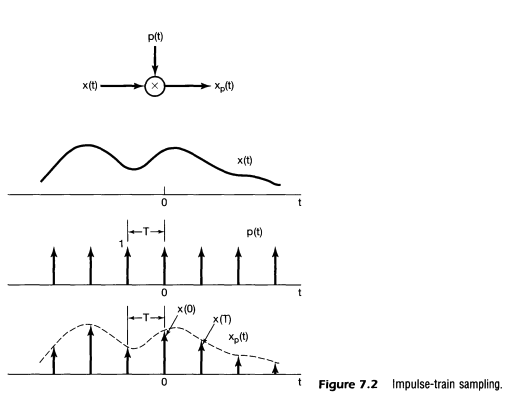
将 $x(t)\delta(t-nT_s)$ 带入傅里叶变换公式，我们就得到一个周期采样的傅里叶变换。

\[\begin{aligned} X(f) & = \int_{t=-\infty}^{\infty} x(t)\delta(t-nT_s) e^{-j2\pi ft}dt \\ & = \sum_{k=-\infty}^{\infty} x(nTs) e^{-j2\pi f(nTs)} \\ & = \sum_{k=-\infty}^{\infty} x(nTs) e^{-j2\pi nf/f_s} \end{aligned}\]

根据傅里叶变换的性质，时域上乘以一个冲击串，相当于频域卷积一个冲击串的傅里叶变换，冲击串的傅里叶变换也是一个冲击串。《信号与系统》教材里说明了，这个结果，就是频域上以 $f_s = T_s$ 为周期重复。

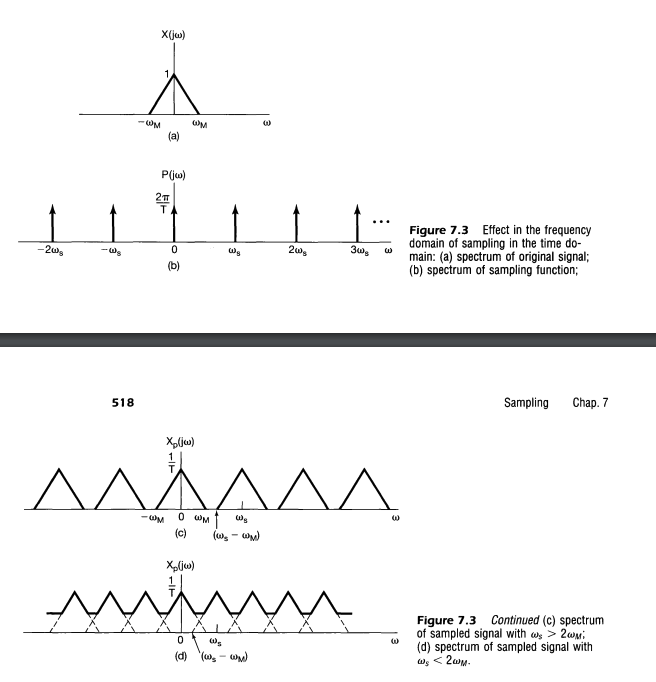
所以时域周期 $T_s$ 采样后的频谱，周期为 $f_s$ 的周期函数，以 $\omega = 2\pi f / f_s$ 归一化频率，我们可以得到归一化频率的离散时间傅里叶变换DTFT公式。

\[\begin{aligned} X(\omega) & = \sum_{k=-\infty}^{\infty} x[n] e^{-j\omega n} \\ x[n] & = \frac{1}{2\pi}\int_{-\pi}^{\pi} X(\omega)e^{j\omega n} d\omega \end{aligned}\]

因为频谱被周期延拓了，实际的有效频谱只在一个周期内（通常取 $-\pi$ 到 $\pi$ ），也就是使用 $-\pi$ 到 $\pi$ 内的频谱作逆变换，即可恢复时域信号。所以DTFT逆变换的积分上下界取的是 $-\pi$ 到 $\pi$。

频域离散化：离散傅里叶变换DFT

DTFT实现了时域的离散化。类似地，我们可以在此基础上实现频域的离散化，也就是对频域进行采样。假设在DTFT的频域上按照 $\omega_k$ 采样, 则时域信号按照 $2\pi/\omega_k$ 周期延拓，于是我们就得到了一对离散信号和他们之间的变换与逆变换，这就是离散傅里叶变换DFT。

\[\begin{aligned} DFT: X[k] & = \sum_{n=0}^{N-1} x[n] e^{-2\pi \frac{k}{N}n} \\ IDFT: x[n] & = \frac{1}{N}\sum_{n=0}^{N-1} X[k] e^{2\pi \frac{k}{N}n} \end{aligned}\]

所以从CTFT到DFT，我们经过几个步骤

  • 时域上按 $T_s$ 周期采样（频域上成为周期为 $f_s = 1/T_s$ 的周期频谱）
  • 时域信号截短成为有限长信号，并作周期 $T_k$ 延拓（也就是频域离散化，采样间隔 $\omega_k = 2 \pi/T_k$ ）
  • 取时域上一个周期、频域上一个周期的序列作为离散傅里叶变化的输入和输出。

可以对比一下以上几种变换的性质：

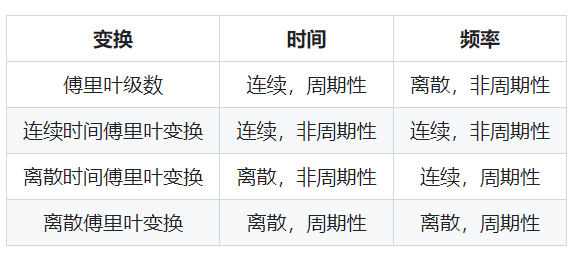
</br>

有了DFT，我们就可以对现实世界的信号进行频率分析啦，而且可以使用数学或软件的手段进行计算加速，成为一种高效的数字信号处理工具。从而衍生出各式各样的数字信号处理的应用，DSP应用主要是围绕这三个阶段：

  • Analysis 分析：从时域到频域的信号变换，如语音到语谱。
  • Filtering 滤波：频域上的操作，如高通、低通、均衡。
  • Synthesis 合成：从频域到时域的逆变换，如从语谱合成语音。

要注意DFT是CTFT的离散化，是对真实连续信号的一种数学近似，从而可以在数字系统中落地。数字系统的离散化、量化是有代价的。时域和频域的采样、截短会带来频谱混叠和频谱泄漏，使用不同精度的数值类型进行运算也会带来不同的量化误差。这些误差的大小就是衡量数字系统的精密程度的指标，是我们工程实现中要时刻考虑的。

DFT的代码实现

从前面的背景知识，我们已经得到N点的DFT变换和逆变换的公式如下，后面就是怎么用代码实现DFT了。

\[\begin{aligned} DFT: X[k] & = \sum_{n=0}^{N-1} x[n] e^{-2\pi \frac{k}{N}n} \\ IDFT: x[n] & = \frac{1}{N}\sum_{n=0}^{N-1} X[k] e^{2\pi \frac{k}{N}n} \end{aligned}\]

上式中时域信号$x[n]$和频域信号$X[k]$都是复数信号。因为计算机的算数运算都是实数运算，我们可以将DFT公式展开成实数运算。首先使用欧拉公式展开复指数：

\[\begin{aligned} X[k] & = \sum_{n=0}^{N-1} x[n] e^{-2\pi \frac{k}{N}n} \\ & = \sum_{n=0}^{N-1} x[n] \left[ \cos(2\pi \frac{k}{N}n) - j\sin(2\pi \frac{k}{N}n)\right] \\ & = \sum_{n=0}^{N-1} \left( x_r[n] + jx_i[n]\right) \left[ \cos(2\pi \frac{k}{N}n) - j\sin(2\pi \frac{k}{N}n)\right] \end{aligned}\]

然后分解实部和虚部，我们就得到了DFT和IDFT实部和虚部计算的四条公式：

\[\begin{aligned} X_r[k] & = \sum_{n=0}^{N-1} \left[ x_r[n]\cos(2\pi \frac{k}{N}n) + x_i[n]\sin(2\pi \frac{k}{N}n)\right] \\ X_i[k] & = \sum_{n=0}^{N-1} \left[-x_r[n]\sin(2\pi \frac{k}{N}n) + x_i[n]\cos(2\pi \frac{k}{N}n)\right] \\ \end{aligned}\] \[\begin{aligned} x_r[n] & = \frac{1}{N}\sum_{n=0}^{N-1} \left[ X_r[k]\cos(2\pi \frac{k}{N}n) - X_r[k]\sin(2\pi \frac{k}{N}n)\right] \\ x_i[n] & = \frac{1}{N}\sum_{n=0}^{N-1} \left[X_r[k]\sin(2\pi \frac{k}{N}n) + X_r[k]\cos(2\pi \frac{k}{N}n)\right] \\ \end{aligned}\]

为了减少计算的时间，我们可以使用空间换时间。在DFT类初始化时，给定DFT的size，并且预创建三角函数表 $t_cos[k][n] = \cos(2\pi \frac{k}{N}n)$ 和 $t_sin[k][n] = \sin(2\pi \frac{k}{N}n)$, 后续每次计算DFT时查表即可。

    for (int i = 0; i < m_size; ++i)
    {
        for (int j = 0; j < m_size; ++j)
        {
            double arg = (double(i) * double(j) * M_PI * 2.0) / m_size;
            m_sin[i][j] = sin(arg);
            m_cos[i][j] = cos(arg);
        }
    }

最后，我们通过下面四条公式即可实现基础的DFT变化和逆变换。

\[\begin{aligned} X_r[k] & = \sum_{n=0}^{N-1} \left( x_r[n]*t\_cos[k][n] + x_i[n]*t\_sin[k][n]\right) \\ X_i[k] & = \sum_{n=0}^{N-1} \left(-x_r[n]*t\_sin[k][n] + x_i[n]*t\_cos[k][n]\right) \\ x_r[n] & = \frac{1}{N}\sum_{n=0}^{N-1} \left( X_r[k]*t\_cos[k][n] - X_i[k]*t\_sin[k][n]\right) \\ x_i[n] & = \frac{1}{N}\sum_{n=0}^{N-1} \left(X_r[k]*t\_sin[k][n] + X_i[k]*t\_cos[k][n]\right) \\ \end{aligned}\]

以下就是按照DFT和IDFT公式实现的C++代码。

void DFT::Forward(const double* real_in, const double* imag_in, double* real_out, double* imag_out) {
    for (int i = 0; i < m_size; ++i) {
        double re = 0.0, im = 0.0;
        for (int j = 0; j < m_size; ++j) re += real_in[j] * m_cos[i][j] + imag_in[j] * m_sin[i][j];
        for (int j = 0; j < m_size; ++j) im -= real_in[j] * m_sin[i][j] - imag_in[j] * m_cos[i][j];
    }
}

void DFT::Inverse(const double* real_in, const double* imag_in, double* real_out, double* imag_out) {
    for (int i = 0; i < m_size; ++i) {
        double re = 0.0, im = 0.0;
        for (int j = 0; j < m_size; ++j) re += real_in[j] * m_cos[i][j] - imag_in[j] * m_sin[i][j];
        for (int j = 0; j < m_size; ++j) im += real_in[j] * m_sin[i][j] + imag_in[j] * m_cos[i][j];
    }
}

实数序列DFT

现实世界采集的信号通常是实数序列，其虚部为零，所以虚部乘法全部可以去掉。于是DFT的公式可以简化如下：

\[\begin{aligned} X_r[k] & = \sum_{n=0}^{N-1} \left[ x_r[n]\cos(2\pi \frac{k}{N}n)\right] \\ X_i[k] & = \sum_{n=0}^{N-1} \left[-x_r[n]\sin(2\pi \frac{k}{N}n)\right] \\ \end{aligned}\]

根据cosine和sine函数的对称性，我们可以得到实数序列DFT的共轭对称性： \(\begin{aligned} X_r[k] & = X_r[N-k] \\ X_i[k] & = -X_i[N-k] \\ X[k] & = X^*[N-k] \end{aligned}\)

比如对于8点的DFT，$X_0, X_1, X_2, X_3, X_4, X_5, X_6, X_7$, 有

\[\begin{aligned} X_1 = X_7^* \\ X_2 = X_6^* \\ X_3 = X_5^* \\ \end{aligned}\]

因此我们只要计算 $X_0, X_1, X_2, X_3, X_4$ 既可以，$X_5, X_6, X_7$ 可以从共轭推导出来。对于N点DFT，假设只考虑偶数N， 那我们只要计算前 $N/2 + 1$ 个点即可。

有了这个性质，对于实数序列DFT, 我们不仅节约了大半计算耗时，还节省接近一半存储空间。

    void DFT::ForwardReal(const double* real_in, double* real_out, double* imag_out)
    {
        for (int i = 0; i < m_size / 2 + 1; ++i)
        {
            double re = 0.0, im = 0.0;
            for (int j = 0; j < m_size; ++j)
                re += real_in[j] * m_cos[i][j];
            for (int j = 0; j < m_size; ++j)
                im -= real_in[j] * m_sin[i][j];
            real_out[i] = re;
            imag_out[i] = im;
        }
    }

而逆变换中，我们需要频域的实部和虚部，计算出时域的实部。

    void DFT::InverseReal(const double* real_in, const double* imag_in, double* real_out)
    {
        for (int i = 0; i < m_size; ++i)
        {
            double re = 0.0;
            for (int j = 0; j < m_bins; ++j)
                re += real_in[j] * m_cos[i][j];
            for (int j = m_bins; j < m_size; ++j)
                re += real_in[m_size - j] * m_cos[i][j];

            for (int j = 0; j < m_bins; ++j)
                re -= imag_in[j] * m_sin[i][j];
            for (int j = m_bins; j < m_size; ++j)
                re -= -imag_in[m_size - j] * m_sin[i][j];

            real_out[i] = re;
        }
    }

DFT性能测试

现在我们来验证一下DFT实现的正确性和计算性能。首先，我们选择一种常用的开源FFT软件KISSFFT作为对比方案。我们记录几个值

  • 对比KISS和my_dft跑一轮变换的时间。
  • 计算my_dft和KISS同一输入的输出结果之间的误差。
  • 计算my_dft先运行DFT，然后对结果作IDFT，恢复的结果与原信号之间的误差。
    start_time = clock();
    my_dft.Forward(in_real, in_imag, out_real, out_imag);
    end_time = clock();


    start_time = clock();
    kiss_fft(forward_fft, in_cpx, out_cpx);
    end_time = clock();

对实序列DFT，作同样的对比

    start_time = clock();
    my_dft.ForwardReal(in_real, out_real, out_imag);
    end_time = clock();

    start_time = clock();
    kiss_fftr(forward_fft, in_real, out_cpx);
    end_time = clock();

以1024点double类型随机数作输入，在一台CPU是2.3Ghz Intel Core i9的Macbook pro 上测试 DFT性能结果如下：

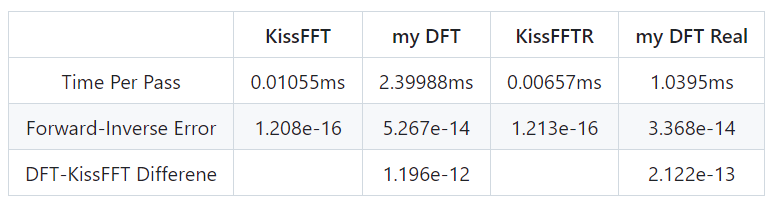
到这里，我们就使用C++实现了一个基础的DFT，可以在程序中实际运行且验证了计算的正确性。但是其计算复杂度是$O(log N^2)$,计算性能离可商用距离还比较遥远。

因此，我们需要引入DFT的计算优化，也就是下一步要讨论的快速傅里叶变换（FFT）。

参考资料

Related Posts