频域LMS自适应滤波

本文代码位于GitHub。

1. 概述
2. LMS和NLMS算法
3. Block LMS算法
4. 快速卷积
5. LMS算法的快速计算：频域自适应滤波
6. 减少时延：滤波器分割的频域自适应滤波

1. 概述

下图是一个典型的自适应滤波场景，输入信号$x(n)$经过一个位置的系统变换$h(z)$后得到参考信号$d(n)$。自适应滤波器的目标是找出一组滤波器系数$w(z)$来逼近系统$h(z)$，使输入信号经过$w(z)$变换后，与参考信号误差最小。

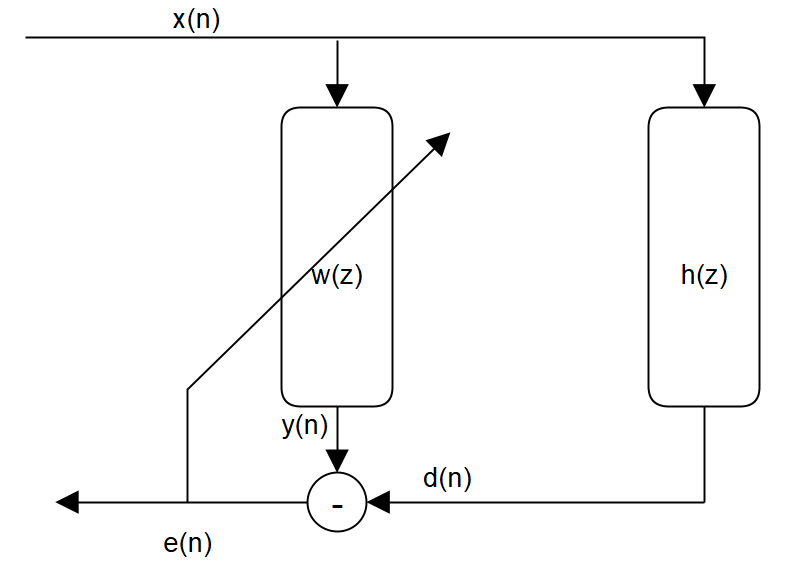
若使用FIR滤波器设计$w(z)$, 自适应滤波器的输出就是输入信号与滤波器权值的卷积：

$y(n)=\sum_{i=0}^{N-1}w_ix(n-i)$

自适应滤波器的算法就是以误差$e(n)$为最小化目标，迭代求出最优的滤波器系数$w(z)$。

$e(n)=d(n)-y(n)$

2. LMS和NLMS算法

LMS是最广泛应用的自适应滤波算法，以MSE误差为目标函数，以梯度下降为优化算法。并且通常情况下，LMS以最新的输入计算的瞬时梯度替代实际梯度计算，类似于机器学习的随机梯度下降法。

NLMS是使用输入的功率对步长进行归一化的方法，可以取得更好的收敛性能。

时域上实现LMS和NLMS算法的参考资料很多，这里不赘述，下面列出算法迭代步骤。

输入:

　输入向量最新样本$\bm{x}(n)$

　期望输出最新样本$\bm{d}(n)$

输出:

　滤波器系数$\bm{w}$,长度为M的FIR滤波器

　滤波器输出$\bm{y}(n)$

　滤波器输出与期望间的误差$e$

初始化:

　滤波器系数$\bm{w}(0)=zeros(1, M)$

迭代过程:

　for n = 0, 1, 2…

　1.读取输入样本$\bm{x}(n)$ 和期望输出样本$\bm{d}(n)$

　2.滤波：

$\bm{y}(n)=\bm{w}^T(n)\bm{x}(n)$

　3.计算误差：

$e(n)=\bm{d}(n) - \bm{y}(n)$

　4.更新系数：

　　LMS:

$\bm{w}(n+1)=\bm{w}(n) + 2\mu e(n)\bm{x}(n)$

　　NLMS:

$\bm{w}(n+1)=\bm{w}(n) + \frac{\mu_0}{\bm{x}^T(n)\bm{x}(n)+\phi} e(n)\bm{x}(n)$

算法复杂度:

　LMS: $2M+1$次乘法和$2M$次加法

　NLMS: $3M+1$次乘法和$3M$次加法

3. Block LMS算法

LMS算法对输入数据是串行处理的，每输入一个样本，都需要进行$2M+1$次乘法和$2M$次加法，对于长度为$N$的信号，计算时间复杂度为$O(NM)$。可以通过将输入数据分段并行处理，并且利用频域FFT来做快速卷积，大大减少计算复杂度。

首先需要将串行的LMS算法转变为分块处理，也就是Block LMS(BLMS)。每次迭代，输入数据被分成长度为$L$的块进行处理。和LMS使用瞬时梯度来进行滤波器参数更新不同，BLMS使用L点的平均梯度来进行参数更新。也就是机器学习里面Stochastic Gradient Descent 和 Mini-Batch Gradient Descent的区别。对第$k$块数据，BLMS算法递推公式为：

$\bm{w}(k+1)=\bm{w}(k) + 2\mu_B \frac{\sum_{i=0}^{L-1}e(kL+i)\bm{x}(kL+i)}{L}$

输入:

　输入向量$\bm{x}$

　期望输出$\bm{d}$

输出:

　滤波器系数$\bm{w}$,长度为M的FIR滤波器

　滤波器输出$\bm{y}$

　滤波器输出与期望间的误差$\bm{e}$

初始化:

　滤波器系数$\bm{w}(0)=zeros(1, M)$

迭代过程:

　for k = 0, 1, 2 … N/L，读入第k块数据$\bm{x}$, $\bm{d}$

　1. $\phi = zeros(1,L)$

　2. for i = 0, 1, 2 … L-1

　　2.1 滤波：

$\bm{y}(kL+i)=\bm{w}^T(k)\bm{x}(kL+i)$

　　2.2 计算误差：

$\bm{e}(kL+i)=\bm{d}(kL+i) - \bm{y}(kL+i)$

　　2.3 累计梯度：

$\phi=\phi+ \mu \bm{e}(kL+i)\bm{x}(kL+i)$

　3 更新系数：

$\bm{w}(k+1)=\bm{w}(k) + \phi$

算法复杂度:

　$2M+1$次乘法和$2M+M/L$次加法

4. 快速卷积

前面一节描述的BLMS算法跟LMS算法相比，除了用块平均梯度代替瞬时梯度外，并没有不同。为了提升卷积计算的复杂度，我们需要引入快速卷积。也就是用FFT计算循环卷积，实现线性卷积的快速分块计算。

长度为L的$x$和长度为M的$w$，线性卷积的结果是长度为$L+M-1$的$y$。时域卷积，频域是相乘，因此有

$y(n)=x(n)*w(n)$ $\mathcal{FT}\left[y(n)\right]= \mathcal{FT}\left[x(n)\right] \mathcal{FT}\left[w(n)\right]$

傅立叶变换在频域上是连续的，计算机做傅立叶运算会将频域离散化采样，转化成$N$点离散傅立叶变换(DFT)，并且用FFT算法做快速计算。将卷积的输入$x$和$w$都补零成$N$点，做一个$N$点的DFT，其逆变换就是循环卷积的结果，时域上是周期为$N$的重复信号。

如上图所示，只有取DFT点数$N>L+M-1$，才能防止卷积结果在时域上面混叠。IDFT结果的前$M+L-1$个值就是所需的卷积结果。

于是两组有限长信号的卷积，则转换成3次DFT计算。

$y(n)= \mathcal{IDFT}\left\{\mathcal{DFT}\left[x(n)\right] \mathcal{DFT}\left[w(n)\right]\right\}$

直接计算卷积，大约需要$N^2$次乘法和$N^2$次加法。

采用FFT算法，3次DFT计算需要$N+\frac{3N}{2}\log_2N$次复数乘法和$3N\log_2N$次复数加法，相对直接计算算法复杂度从$O(N^2)$降到了$O(N\log_2N)$。

前面说的是两段有限长信号作一次卷积的流程。回到BLMS，对信号$x$进行分段处理。每段输入长度是$B$，滤波器长度是$M$。

如果在$w$后面补$K-B$个零，而在$x$当前块前部保留前一块的最后$K-B$个点，做$K$点快速卷积，结果中最后$B$点是有效输出，而前$K-B$点可丢弃。这种分块处理长卷积的方法，叫Overlap-and-Save方法。用FFT快速卷积+Overlap-and-Save方法，就可以高效处理BLMS滤波。

5. LMS算法的快速计算：频域自适应滤波

使用快速卷积的方法实现BLMS，就是频域实现的LMS自适应滤波器。称作Fast Block LMS (FBLMS) 或者 Frequency Domain Adaptive Filter (FDAF)。

对于长度为$M$的滤波器，FBLMS一般采用$2M$点FFT，且使用Overlap-and-Savee的快速卷积方法。也就是说，滤波器向量$w$做FFT前须补$M$个零值。

$W=FFT\left[ \begin{matrix} w\\ 0 \end{matrix} \right]$

输入向量的分块长度也设为$M$，则FFT的输入前$M$点是保存前一块的数据，后$M$点是当前块数据。

$X=FFT\left[ \begin{matrix} x_{k-1}\\ x_k \end{matrix} \right]$

使用overlap-save快速卷积方法实现BLMS中的卷积部分，当前块输出向量$y$为IFFT的后$M$点。

$\left[ \begin{matrix} C\\ y_k \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} w\\ 0 \end{matrix} \right] FFT\left[ \begin{matrix} x_{k-1}\\ x_k \end{matrix} \right]\right]$

梯度的计算，可以将误差与输入信号放到频域来做，具体推导参考Block Adaptive Filters and Frequency Domain Adaptive Filters

$\left[ \begin{matrix} \phi\\ D \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} 0\\ e \end{matrix} \right] FFT\left[ \begin{matrix} x_{k-1}\\ x_k \end{matrix} \right]'\right]$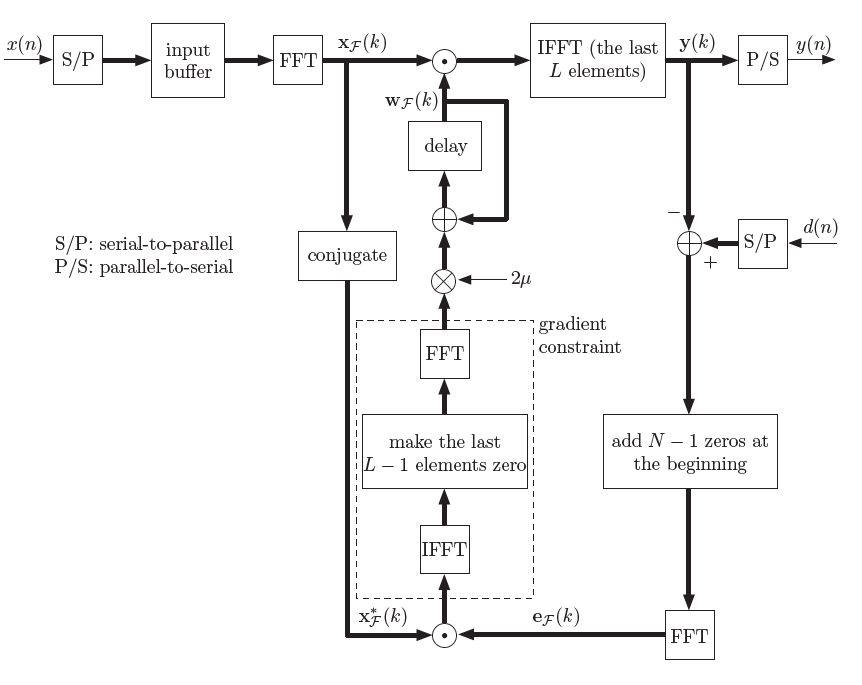

输入:

　分块输入信号$\bm{x_k}$, 块长度为M

　分块参考信号$\bm{d_k}$, 块长度为M

输出:

　更新的滤波器系数$\bm{w_k}$,长度为M的FIR滤波器

　分块输出信号$\bm{y_k}$, 块长度为M

　滤波器输出与参考信号间的误差$\bm{e}$

初始化:

　滤波器系数$\bm{w}_0=zeros(M,1)$

　初始数据块$\bm{x}_0=zeros(M,1)$

迭代过程:

　for $k = 1, 2 … N/L$，读入第$k$块数据$\bm{w_k}$, $\bm{d_k}$

　1. $\bm{\phi} = zeros(M,1)$

　2. 计算块输出

$\left[ \begin{matrix} C\\ y_k \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} w_k\\ 0 \end{matrix} \right] FFT\left[ \begin{matrix} x_{k-1}\\ x_k \end{matrix} \right]\right]$

　3. 计算误差： $\bm{e} = \bm{y}_k - \bm{d}_k$

　4. 计算梯度：

$\left[ \begin{matrix} \phi\\ D \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} 0\\ e \end{matrix} \right] \overline{FFT\left[ \begin{matrix} x_{k-1}\\ x_k \end{matrix} \right]}\right]$

　5. 更新滤波器：

$FFT\left[ \begin{matrix} w_{k+1}\\ 0 \end{matrix} \right]= FFT\left[ \begin{matrix} w_k\\ 0 \end{matrix} \right] + \mu FFT\left[ \begin{matrix} \phi\\ 0 \end{matrix} \right]$

算法复杂度:

　$10M\log M+26M$

def process(self, x_b, d_b, update=True): 
	'''
	Process a block data, and updates the adaptive filter (optional)
	
	Parameters
	----------
	x_b: float
	the new input block signal
	d_b: float
	the new reference block signal
	update: bool, optional
	whether or not to update the filter coefficients
	'''  
	self.x = np.concatenate([self.x[self.B:], x_b])
	
	# block-update parameters
	X = fft(self.x)
	y_2B = ifft( X * self.W)
	y = np.real(y_2B[self.B:])
	
	e = d_b - y
	
	# Update the parameters of the filter
	if self.update:
	E = fft(np.concatenate([np.zeros(self.B), e])) # (2B)
	
	if self.nlms:
	norm = np.abs(X)**2 + 1e-10
	E = E/norm
	# Set the upper bound of E, to prevent divergence
	m_errThreshold = 0.2
	Enorm = np.abs(E) # (2B)
	# print(E)
	for eidx in range(2*self.B):
	if Enorm[eidx]>m_errThreshold:
	E[eidx] = m_errThreshold*E[eidx]/(Enorm[eidx]+1e-10) 
	
	# Compute the correlation vector (gradient constraint)
	phi = np.einsum('i,i->i',X.conj(),E) # (2B)
	phi = ifft(phi)
	phi[self.B:] = 0
	phi = fft(phi)
	
	self.W = self.W + self.mu*phi
	self.w = np.real(ifft(self.W)[:self.B]) 
	
return y, e

6. 减少时延：滤波器分割的频域自适应滤波

前面是将输入信号分块处理，提高算法效率。当FIR滤波器抽头数量很大时，FBLMS每M点计算一次输出和更新滤波器，造成比较大的延时。

一种想法是将滤波器也进行分割，这种改进延时的滤波器有几种名字： Partitioned Fast Block LMS (PFBLMS)，Frequency Domain Adaptive Filter (PBFDAF)， Multi-DelayBlock Filter(MDF)，都是一回事。

如果将长度为$M$的滤波器$w$等分为长度为$B$的小段，$M=P*B$。则卷积的结果可以分解为$P$个卷积之叠加。

$y(n)=\sum_{l=0}^{P} y_l(n)$ $y_l(n)=\sum_{i=0}^{B-1} w_{i+lB}x(n-lB-i)$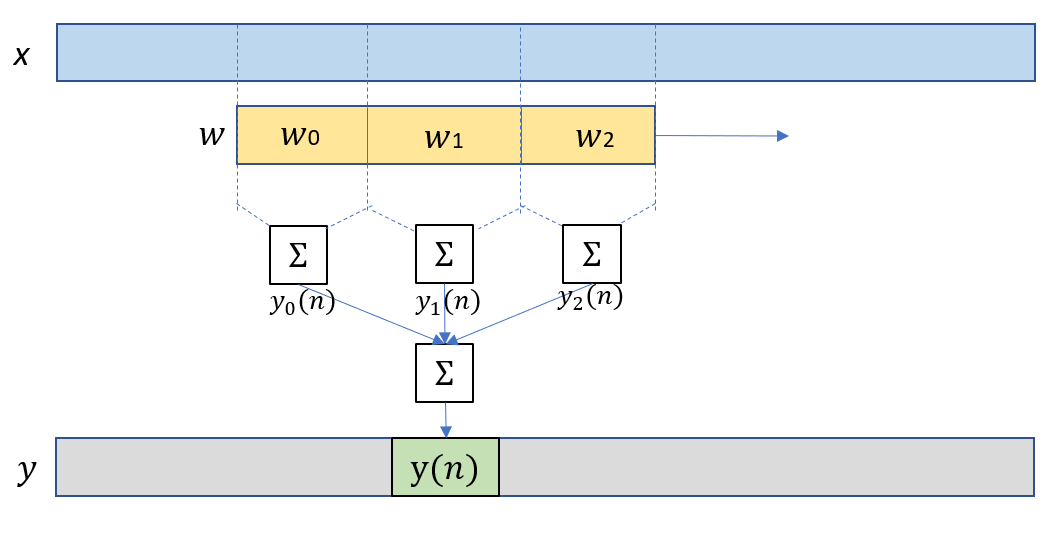

于是一段线性卷积被分解成$P$个线性卷积，并且可以用FFT+OLS分别计算这$P$个卷积。这样做好处是，每次迭代只需要输入长度为$B$的信号块，保留原buffer中的后$P-1$段，与最新的一段作为新的输入，就可以重复以上的$P$段卷积叠加。每次迭代，可以更新$B$点输出信号。

PFBLMS算法的时延就只有FBLMS的$1/P$，极大地改善了滤波器的可用性。Speex和WebRTC的回声消除代码都使用了这种结构的滤波器。

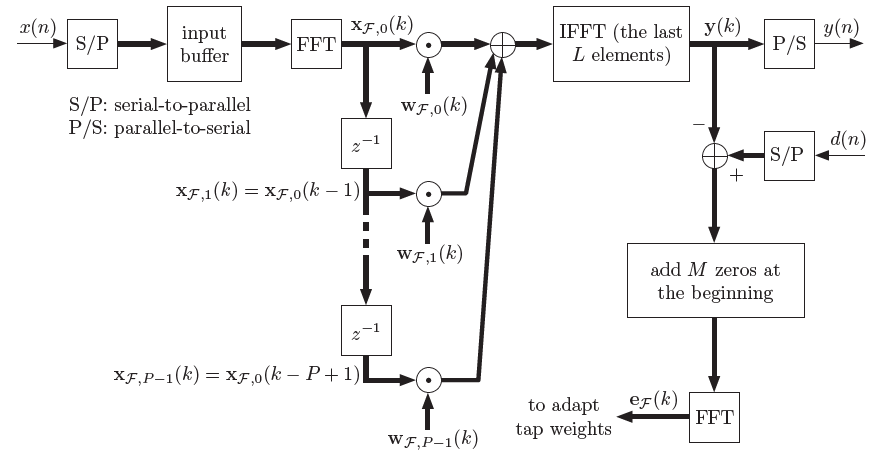
输入:

　分块输入信号$\bm{x_k}$, 块长度为B

　分块参考信号$\bm{d_k}$, 块长度为B

输出:

　滤波器系数$\bm{w}$,长度为M=PB的FIR滤波器

　分块输出信号$\bm{y_k}$, 块长度为B

　滤波器输出与期望间的误差$\bm{e}$

初始化:

　滤波器系数$\bm{w}_0=zeros(B,P)$

　初始数据块$\bm{x}_0=zeros(B,P)$

迭代过程:

　for k = 0, 1, 2 … N/B，读入第k块数据$x_k$, $d_k$

　1. $\bm{\phi} = zeros(B,1)$

　2. 滑动重组输入信号，并且计算FFT。

　（实际只需计算最后一列，前P-1列可以使用上一次迭代保留结果）

$Xf_k = FFT\left[ \begin{matrix} x_{k-P}&...& x_{k-2} & x_{k-1}\\x_{k-P+1}&...& x_{k-1} & x_k \end{matrix} \right]$

　2. 计算块输出

$\left[ \begin{matrix} C\\ y_k \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} w_k\\ 0 \end{matrix} \right] Xf_k\right]$

　3. 计算误差： $e = y_k - d_k$

　4. 计算梯度：

$\left[ \begin{matrix} \phi\\ D \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} 0\\ e \end{matrix} \right] \overline{Xf_k}\right]$

　5. 更新滤波器：

$FFT\left[ \begin{matrix} w_{k+1}\\ 0 \end{matrix} \right]= FFT\left[ \begin{matrix} w_k\\ 0 \end{matrix} \right] + \mu FFT\left[ \begin{matrix} \phi\\ 0 \end{matrix} \right]$

算法复杂度:

　与FBLMS相仿

def process(self, x_b, d_b, update=True): 
    '''
	Process a block data, and updates the adaptive filter (optional)
	
	Parameters
	----------
	x_b: float
	the new input block signal
	d_b: float
	the new reference block signal
	update: bool, optional
	whether or not to update the filter coefficients
	'''
	self.x = np.concatenate([self.x[self.B:], x_b])
	Xf_b = fft(self.x)
	
	# block-update parameters
	self.Xf[1:] = self.Xf[:self.M-1] # Xf : Mx2B  sliding window
	self.Xf[0] = Xf_b # Xf : Mx2B  sliding window
	y_2B = ifft(np.sum(self.Xf * self.Wf, axis=0)) # [Px2B] element multiply [Px2B] , then ifft
	y = np.real(y_2B[self.B:])
	
	e = d_b - y
	
	if update:
	E = fft(np.concatenate([np.zeros(self.B), e])) # (2B)
	
	if self.nlms:
	norm = np.abs(Xf_b)**2 + 1e-6
	E = E/norm
	
	# Set the upper bound of E, to prevent divergence
	m_errThreshold = 0.2
	Enorm = np.abs(E) # (2B)
	# print(E)
	for eidx in range(2*self.B):
	if Enorm[eidx]>m_errThreshold:
	E[eidx] = m_errThreshold*E[eidx]/(Enorm[eidx]+1e-10)    
	
	
	# Update the parameters of the filter
	self.Wf = self.Wf + self.mu*E*self.Xf.conj()
	
	# Compute the correlation vector (gradient constraint)
	if self.constrained:
	waux = ifft(self.Wf, axis=1)
	waux[:, self.B:] = 0
	self.Wf = fft(waux, axis=1)
	
	self.w = np.real(ifft(self.Wf, axis=1)[:, :self.B].flatten())
return y, e

参考文献

[1] B. Farhang-Boroujeny, Adaptive Filters: theory and applications. John Wiley & Sons, 2013.

[2] Block Adaptive Filters and Frequency Domain Adaptive Filters

wjchen

频域LMS自适应滤波

1. 概述

2. LMS和NLMS算法

3. Block LMS算法

4. 快速卷积

5. LMS算法的快速计算：频域自适应滤波

6. 减少时延：滤波器分割的频域自适应滤波

Related Posts