1. 概述
Speex AEC是开源的回声消除代码。 回声消除框架图如下
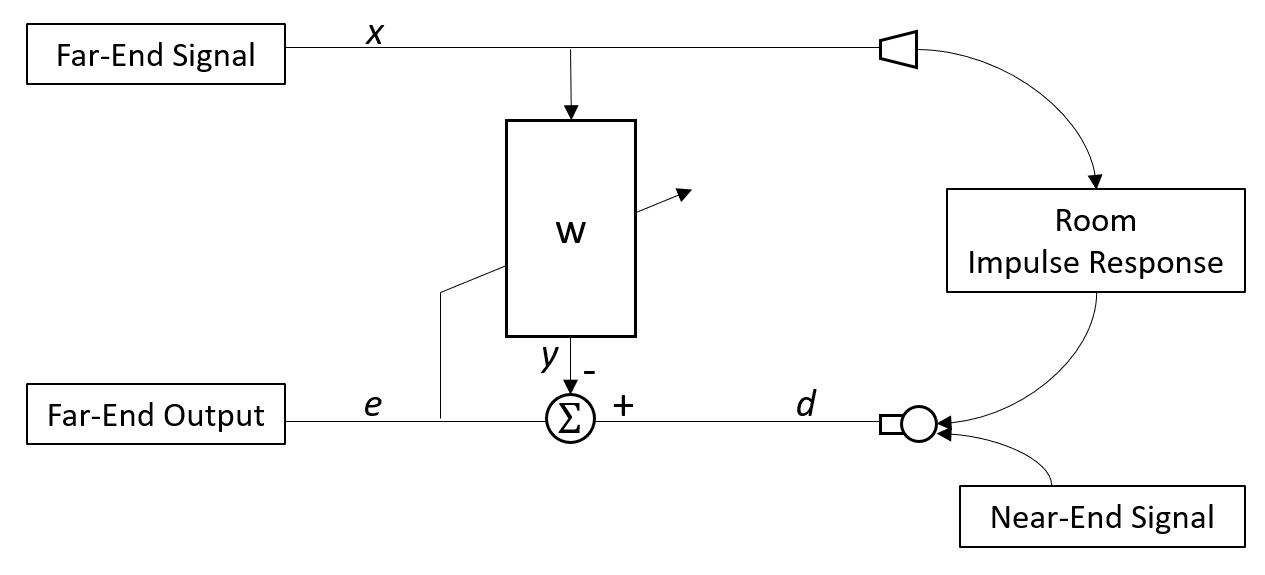
AEC一般的方法使用自适应FIR滤波器设计$w(z)$:
\[y(n)=\sum_{i=0}^{N-1}w_ix(n-i)\]自适应滤波器的算法的的目标误差$e(n)$,也是回声消除后的近端输出信号。
\[e(n)=d(n)-y(n)\]Speex的信号处理部分单独分成一个项目SpeexDSP, 在以下地址:https://github.com/xiph/speexdsp
SpexxDSP包括了回声消除、语音去噪、AGC等,其中回声消除代码在mdf.c。而Github上有mdf.c的MATLAB实现版本,分析算法时使用MATLAB分析更直接些,地址在 https://github.com/wavesaudio/Speex-AEC-matlab
Speex AEC算法特点包括几个方面:
-
自适应滤波器使用MDF滤波器
-
双滤波器结构
-
自适应滤波器步长优化
-
残留回声消除
2. MDF滤波器
Speex AEC 的滤波部分主要是基于[1] Multidelayblock frequency domain adaptive filter所提出的MDF结构。我的另外一篇博文《频域LMS自适应滤波》说过, MDF和PBFDAF、PFBLMS是一回事,也就是将FIR滤波器分割的频域LMS滤波。
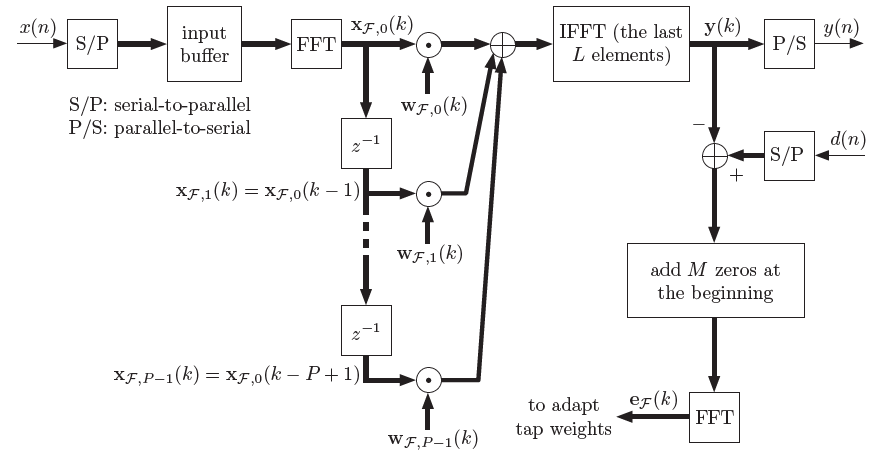
MDF主要包括三个方面:
1 将输入信号分块处理,使用Overlap-and-Save方法计算卷积的分块结果。 2 分块卷积转入频域计算,使用FFT将计算复杂度从$O(N^2)$降到$O(N\log_2 N)$。 3 进一步将FIR滤波器系数进行分段,一组卷积分解为多组卷积之和。输入和输出的分块长度变短,大大减小滤波器时延。
论文[1]中MDF步骤总结为以下7条公式。

这七条公式跟我之前的博文总结的迭代过程可一一对应:
公式1、2对应迭代过程步骤2,计算块输入的FFT,并且滑动保存P块结果。
公式3对应迭代步骤2。
公式4、5、6对应迭代步骤3、4。
公式7对应迭代步骤5。
迭代过程:
for k = 0, 1, 2 … N/B,读入第k块数据$x_k$, $d_k$
1. $\bm{\phi} = zeros(B,1)$
2. 滑动重组输入信号,并且计算FFT。
(实际只需计算最后一列,前P-1列可以使用上一次迭代保留结果)
\[Xf_k = FFT\left[ \begin{matrix} x_{k-P}&...& x_{k-2} & x_{k-1}\\x_{k-P+1}&...& x_{k-1} & x_k \end{matrix} \right]\]2. 计算块输出
\[\left[ \begin{matrix} C\\ y_k \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} w_k\\ 0 \end{matrix} \right] Xf_k\right]\]3. 计算误差: $e = y_k - d_k$
4. 计算梯度:
\[\left[ \begin{matrix} \phi\\ D \end{matrix} \right]=IFFT\left[ FFT\left[ \begin{matrix} 0\\ e \end{matrix} \right] \overline{Xf_k}\right]\]5. 更新滤波器:
\[FFT\left[ \begin{matrix} w_{k+1}\\ 0 \end{matrix} \right]= FFT\left[ \begin{matrix} w_k\\ 0 \end{matrix} \right] + \mu FFT\left[ \begin{matrix} \phi\\ 0 \end{matrix} \right]\]2. 双滤波器结构与双讲检测
Speex 除了使用MDF作自适应滤波,还是用了双滤波器结构(Two-Path Method)[3][4]。 双滤波器结构包括一个迭代更新的自适应Background Filter, 和一个非自适应的Foreground Filter。在自适应滤波器性能变坏、甚至发散时, AEC使用Foreground Filter的结果,并且重置Background Filter。 在Background Filter 性能变好时,将其参数下载到Foregound Filter。
这种双滤波器结构,可以实现隐式的双讲检测。 在双讲的情况下,Background Filter无法收敛,其更新结果不会保存下来,也就实现了区分双讲和非双讲的目标。
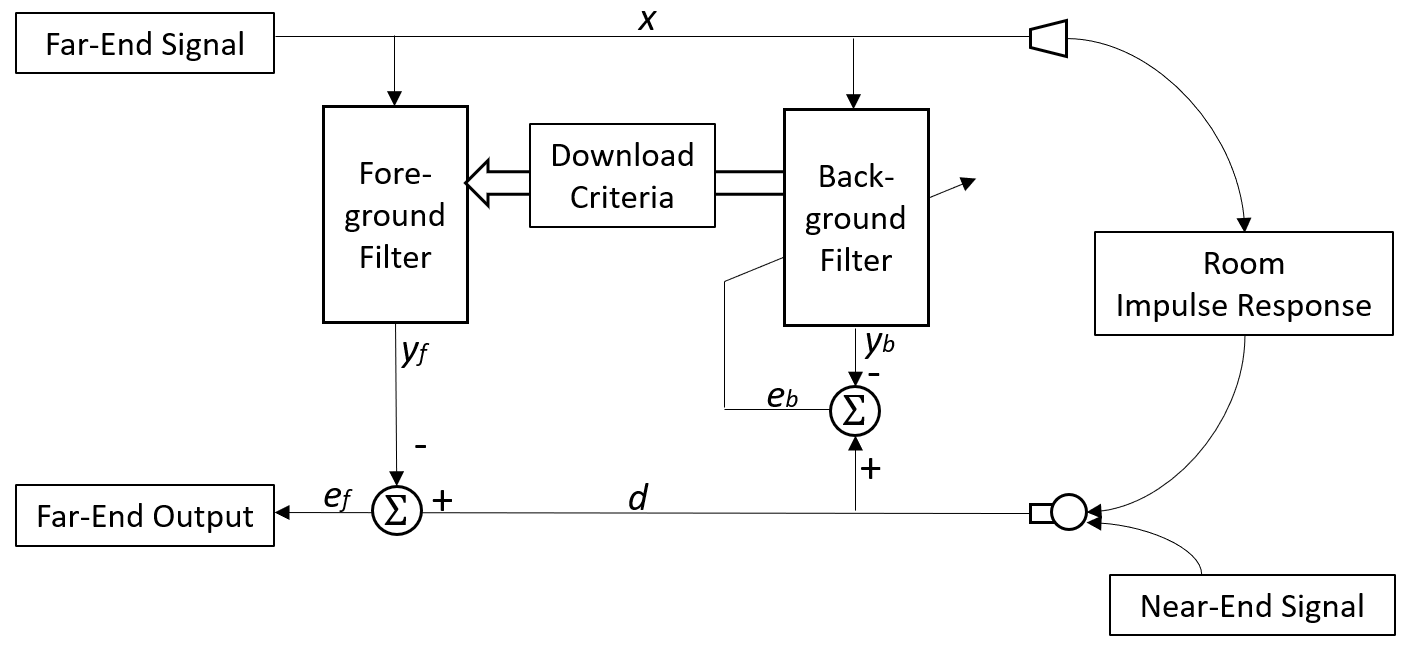
上图就是典型的双滤波器AEC结构,其核心就是将Background Filter下载到Foregound Filter的判决标准。一般而言,可以有着几方面的考虑:
- $\sigma_{x}^2>T_{1}$: 远端信号是否足够大,如果远端信号功率很小,就可以认为不会产生回声,无需更新滤波器。
- $\sigma_{m}^2>T_{1}$: 近端麦克风信号是否足够大,如果近端信号功率很小,则认为既没有采集到回声和近端语音,无需更新滤波器。
- $\frac{\sigma_{ef}^2}{\sigma_{eb}^2}>T_3$, Background Filter 误差比Foreground Filter误差小,性能更优。
- $\frac{\sigma_{m}^2}{\sigma_{eb}^2}>T_4$, 保证Background Filter ERLE大于一定值才使用。
- $\xi_{DTD}>T_5$, 衡量双讲的可能性,双讲会导致自适应滤波器发散,只有非双讲情况下才更新Foreground Filter.
Speex AEC使用的判决准则,可以从代码里面提炼出来,跟以上提到的几点不完全一样,是用Foreground Filter和Background Filter输出的残留功率之差来进行判别,
\[(Sff-See)*abs(Sff-See) > (Sff*Dbf)\]其中$Sff$是Foreground Filter与麦克风信号之差的功率,$See$是Background Filter与麦克风信号之差的功率, Dbf是两个Filter输出信号之差的平方。 于是判别公式可以写成
\[(e_f^2-e_b^2)|e_f^2-e_b^2|> e_f^2|e_f - e_b|^2\]这个判决准则的数学原理暂没有深究,其代码如下。
% Logic for updating the foreground filter */
% For two time windows, compute the mean of the energy difference,
as well as the variance */
VAR1_UPDATE = .5;
VAR2_UPDATE = .25;
VAR_BACKTRACK = 4;
MIN_LEAK = .005;
st.Davg1 = .6*st.Davg1 + .4*(Sff-See);
st.Davg2 = .85*st.Davg2 + .15*(Sff-See);
st.Dvar1 = .36*st.Dvar1 + .16*Sff*Dbf;
st.Dvar2 = .7225*st.Dvar2 + .0225*Sff*Dbf;
update_foreground = 0;
% Check if we have a statistically significant reduction in the residual echo */
% Note that this is *not* Gaussian, so we need to be careful about the longer tail */
if (Sff-See)*abs(Sff-See) > (Sff*Dbf)
update_foreground = 1;
elseif (st.Davg1* abs(st.Davg1) > (VAR1_UPDATE*st.Dvar1))
update_foreground = 1;
elseif (st.Davg2* abs(st.Davg2) > (VAR2_UPDATE*(st.Dvar2)))
update_foreground = 1;
end
如果Background Filter过于发散,则应该重置,可将其重置为Foreground Filter。 其MATLAB代码如下:
% Do we update? */
if (update_foreground)
st.Davg1 = 0;
st.Davg2 = 0;
st.Dvar1 = 0;
st.Dvar2 = 0;
st.foreground = st.W;
% Apply a smooth transition so as to not introduce blocking artifacts */
for chan = 1:C
st.e(st.frame_size+1:N, chan) = (st.window(st.frame_size+1:N) .* st.e(st.frame_size+1:N, chan)) + (st.window(1:st.frame_size) .* st.y(st.frame_size+1:N, chan));
end
else
reset_background=0;
% Otherwise, check if the background filter is significantly worse */
if (-(Sff-See)*abs(Sff-See)> VAR_BACKTRACK*(Sff*Dbf))
reset_background = 1;
end
if ((-st.Davg1 * abs(st.Davg1))> (VAR_BACKTRACK*st.Dvar1))
reset_background = 1;
end
if ((-st.Davg2* abs(st.Davg2))> (VAR_BACKTRACK*st.Dvar2))
reset_background = 1;
end
if (reset_background)
% Copy foreground filter to background filter */
st.W = st.foreground;
% We also need to copy the output so as to get correct adaptation */
for chan = 1:C
st.y(st.frame_size+1:N, chan) = st.e(st.frame_size+1:N, chan);
st.e(1:st.frame_size, chan) = st.input(:, chan) - st.y(st.frame_size+1:N, chan);
end
See = Sff;
st.Davg1 = 0;
st.Davg2 = 0;
st.Dvar1 = 0;
st.Dvar2 = 0;
end
end
3. 自适应滤波器步长优化
自适应滤波器优化的一种思路是吧固定步长优化成可变步长,并且通过当前的各段信号,推导出最优步长。
网上有博文 爱酷媒: Speex回声消除原理深度解析 很好地对此进行了推导,主要是基于论文 On Adjusting the Learning Rate in Frequency Domain Echo Cancellation With Double-Talk [5].
下面摘录其中的主要结论。 最优步长等于残余回声方差与误差信号方差之比
\[\mu_{opt} = \frac{\sigma_r^2}{\sigma_e^2}\]为了计算残留回声的功率,定义泄漏因子$\eta$, 取值在0~1之间 \(\sigma_r^2 = \eta \sigma_Y^2\)
泄漏因子通过递归平均更新:

4. 残留回声消除 Residual Echo Cancellation
自适应滤波器不能百分百消除回声,AEC的输出信号含有残留的回声信号,这个时候就需要一个Post-Filter,进行残留回声消除(Residual Echo Cancellation)。 Speex是将残留回声消除和噪声消除放在同一个模块中处理,代码在preprocessor.c。

如上图所示,麦克风输入信号通常包括几部分,近端语音$s$, 近端噪声$n$, 自适应滤波的目标回声$d$。 于是AEC的输出误差信号为
\[e = (d-y) + s + n\]其中$d-y$就是残留回声信号。残留回声的功率通过泄漏因子计算:
\[\sigma_r^2 = \eta \sigma_Y^2\]Speex在preprocessor.c中,将Post Filter实现为一个统计信号处理估计的噪声抑制器,近端噪声、残留回声、混响均视作噪声,将其功率求和,得到总噪声功率。
/* Total noise estimate including residual echo and reverberation */
spx_word32_t tot_noise = ADD32(ADD32(ADD32(EXTEND32(1), PSHR32(st->noise[i],NOISE_SHIFT)) , st->echo_noise[i]) , st->reverb_estimate[i]);
后面就是语音增强的内容,利用当前帧的噪声功率、,估算后验信噪比和先验信噪比,最后通过统计方法求得抑制增益Gain。 Gain和Post-Filter的收入信号相乘,就得到去噪后的信号,是对近端语音的一种估计。
Speex使用MCRA法更新噪声功率、判决引导法计算噪声概率、MMSE-LSA法计算噪声抑制增益。原理可以参考我前面两篇博文。 单通道语音增强之综述 单通道语音增强之统计信号模型
参考文献
[1] J.-S. Soo and K. K. Pang, “Multidelay block frequency domain adaptive filter,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 38, no. 2, pp. 373–376, 1990.
[2] B. Farhang-Boroujeny, Adaptive filters: theory and applications. John Wiley & Sons, 2013.
[3] M. A. Iqbal and S. L. Grant, “Novel and efficient download test for two path echo canceller,”in 2007 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics. IEEE,2007, pp. 167–170.
[4] F. Lindstrom, C. Schuldt, and I. Claesson, “An improvement of the two-path algorithm transfer logic for acoustic echo cancellation,” IEEE transactions on audio, speech, and language processing, vol. 15, no. 4, pp. 1320–1326, 2007.
[5] Valin J M. On adjusting the learning rate in frequency domain echo cancellation with double-talk[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(3): 1030-1034.
[7] 单通道语音增强之综述