• 1. 预备知识
  • 1.1 高斯分布
  • 1.2 Jensen不等式
  • 1.3 矩阵求导
• 2.高斯混合模型和EM算法
  • 2.1 高斯混合模型(GMM)
  • 2.2 EM算法
• 3.EM算法解单变量GMM
  • 3.1 E-Step:
  • 3.2 M-Step:
• 4.EM算法解多变量GMM
  • 4.1 E-Step:
  • 4.2 M-Step:
• 5.总结

1. 预备知识

1.1 高斯分布

高斯分布是拟合随机数据最常用的模型。单变量$x$的高斯分布概率密函数如下:

$$\textit{N}(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]$$

其中

• $\mu $ 分布的数学期望,

• $\sigma$ 标准差, $ \sigma ^{2}$ 是方差.

更一般的情况，如果数据集是d维的数据, 就可以用多变量高斯模型来拟合。概率密度是:

$$\textit{N}(x; \mu, \Sigma) = \frac{1}{\sqrt{(2\pi)^d\det(\Sigma)}}\exp\left[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right]$$

其中

• $x$是一个d×N的向量, 代表N组d维数据,
• $\mu$是一个d×1 的向量, 代表每维的数学期望,
• $\Sigma$是一个d×d的矩阵, 代表模型的协方差矩阵

1.2 Jensen不等式

这里给出随机分析里面Jensen’s不等式的结论。在EM算法的求解过程中，Jensen不等式可以简化目标函数。

定理. 对一个凸函数$f$和随机变量$x$:

$$f\left[E(x)\right] \leq E\left[f(x)\right]$$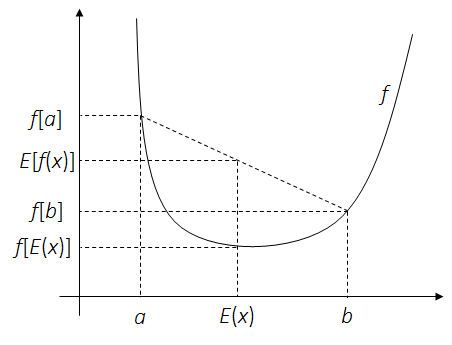

定理. 对一个凹函数$f$和随机变量$x$:

$$f\left[E(x)\right] \geq E\left[f(x)\right]$$

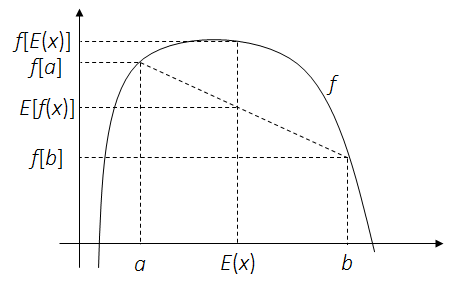
1.3 矩阵求导

多维高斯混合模型的求解需要借助于矩阵和向量求导的公式。 下面是从 《The Matrix Cookbook》一书中摘录在推导过程中可能会用到的公式。

$$\begin{aligned} \frac{\partial x^Ta}{\partial x} &= \frac{\partial a^Tx}{\partial x} = a\\ \frac{\partial x^TBx}{\partial x} &= (B + B^T )x\\ \frac{\partial (x -s)^TW(x-s)}{\partial x} &= -2W(x-s), \text{ (W是对称矩阵)} \\ \frac{\partial a^TXa}{\partial X} &= \frac{\partial a^TX^Ta}{\partial X} = aa^T\\ \frac{\partial \det(X)}{\partial X} &= \det(X)(X^{-1})^T\\ \frac{\partial \ln \det(X)}{\partial X} &= (X^{-1})^T\\ \frac{\partial \det(X^{-1})}{\partial X} &= -\det(X^{-1})(X^{-1})^T\\ \frac{\partial \ln \det(X)}{\partial X^{-1}} &= \frac{\partial \ln \det(X)}{\partial \det(X)}\frac{\partial \det(X)}{\partial X^{-1}} \\ &= \frac{1}{\det(X)}\left[-\det(X)X^T\right]\\ &= -X^T\\ \frac{\partial Tr(AXB)}{\partial X} &= A^TB^T\\ \frac{\partial Tr(AX^-1B)}{\partial X} &= -(X^{-1}BAX^{-1})^T \end{aligned}$$

2.高斯混合模型和EM算法

2.1 高斯混合模型(GMM)

现实采集的数据是比较复杂的，通常无法只用一个高斯分布拟合，而是可以看作多个随机过程的混合。可定义高斯混合模型是$K$个高斯分布的组合，用以拟合复杂数据。

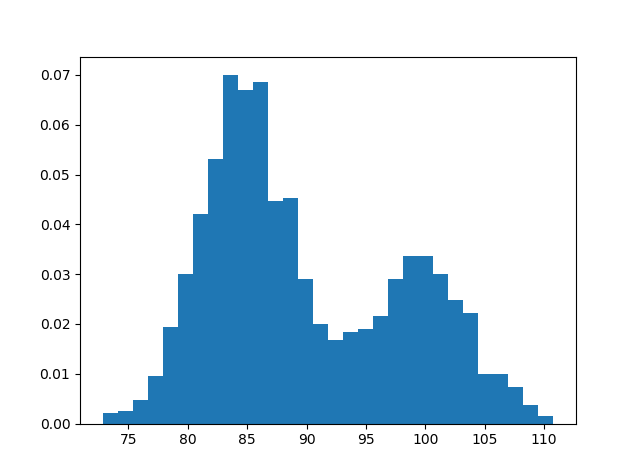
假设有一个数据集，包含了$N$个相互独立的数据：$x = {x_1, x_2 …x_i… x_N}$, 这些数据看起来有$K$个峰，这样的数据集可用以下定义的高斯混合模型拟合：

$$p(x|\Theta) = \sum_{k}^{}\alpha_{k}\textit{N}(x; \mu_k, \sigma_k) = \sum_{k}^{}\alpha_{k}\frac{1}{\sqrt{2\pi\sigma_k^2}}\exp\left[-\frac{(x-\mu_k)^2}{2\sigma_k^2}\right]$$

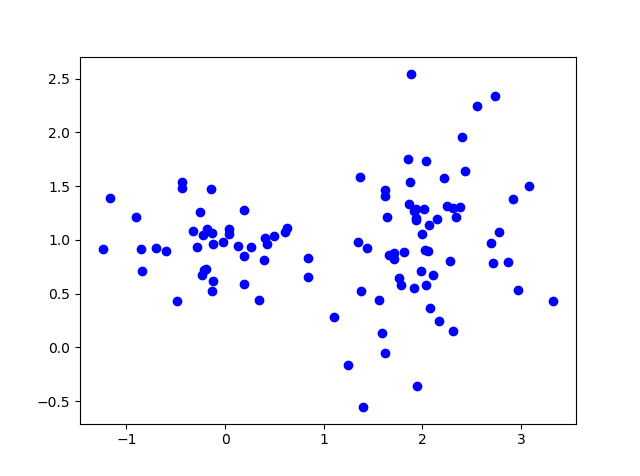
如果每一个数据点$x_i$都是d维的, 这些数据$x$如上图看起来分散在$K$个聚类，这种数据集可以用多变量高斯混合模型拟合。

$$\begin{aligned} p(x|\Theta) &= \sum_{k}^{}\alpha_{k}\textit{N}(x; \mu_k, \Sigma_k) \\ &= \sum_{k}^{}\alpha_{k}\frac{1}{\sqrt{(2\pi)^d\det(\Sigma_k)}}\exp\left[-\frac{1}{2}(x-\mu_k)^T\Sigma_{k}^{-1}(x-\mu_k)\right] \end{aligned}$$

其中$\Theta$ 代表全体高斯模型参数, $\alpha_k$ 是第$k$个高斯模型的先验概率, 各个高斯模型的先验概率加起来等于1。

$$\sum_{k}\alpha_k = 1$$

2.2 EM算法

EM 算法是一种迭代的算法，算法解决的问题可如下表述：

• 采集到一组包含$N$个独立数据的数据集$x$。
• 预先知道、或者根据数据特点估计可以用$K$个高斯分布混合进行数据拟合。
• 目标任务是估计出高斯混合模型的参数：$K$组($\alpha_{k}$, $\mu_k$, $\sigma_k$), 或 ($\alpha_{k}$, $\mu_k$, $\Sigma_{k}$).

似然函数:

对于相互独立的一组数据, 最大似然估计(MLE)是最直接的估计方法。$N$个数据点的总概率可以表述成每个数据点的概率之乘积，这被称作似然函数

$$p(x|\Theta) = \prod_{i}p(x_i|\Theta)$$

最大似然估计通过求似然函数的极大值，来估计参数$\Theta$。

$$\Theta = \argmax_{\Theta} \prod_{i}p(x_i|\Theta)$$

对高斯混合模型使用最大似然估计，求得的似然函数是比较的复杂的，单变量和多变量GMM似然函数结果如下，可以看到多变量GMM似然函数涉及多个矩阵的求逆和乘积等运算。所以要准确估计出$K$组高斯模型的参数，是很难的。

$$p(x|\Theta) = \prod_{i}p(x_i|\Theta) = \prod_{i}\left[\sum_{k}\alpha_{k}\textit{N}(x_i| \mu_k, \sigma_k) \right]$$ $$p(x|\Theta) = \prod_{i}p(x_i|\Theta) = \prod_{i}\left[\sum_{k}\alpha_{k}\textit{N}(x_i| \mu_k, \Sigma_k)\right]$$

GMM 似然函数首先可以通过求对数进行简化，把乘积变成和。和的形式更方便求导和求极值。

$$L(x|\Theta) = \sum_{i}\ln\left[p(x_{i}|\mu_k, \sigma_k) \right] = \sum_{i}\ln\left[\sum_{k}\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k) \right]$$

隐参数:

是否对前面的对数似然函数进行求极大值，就可以求出目标的$K$组高斯模型参数了呢？我看到公式里面有两重求和，其中一重是在对数函数里面，直接求极值并不可行。

EM算法提出了用迭代逼近的方法，来对最优的高斯混合模型进行逼近。为了帮助迭代算法的过程，EM算法提出了隐参数$z$, 每次迭代，先使用上一次的参数计算隐参数$z$的分布，然后使用$z$更新似然函数，对目标参数进行估计。 在GMM估计问题中，EM算法所设定的隐参量$z$ 一般属于${1 ,2 … k … K}$. 用于描述计算出GMM中$K$组高斯模型的参数后，某个数据点$x_i$属于第$z$个高斯模型的概率:

$$p(z|x_{i}, \mu_k, \sigma_k)$$

把隐参量$x$引入到第$i$个数据的概率估计中：

$$p(x_{i}|\Theta) = \sum_{k} p(x_{i}|z=k,\mu_k, \sigma_k) p(z=k) \\$$

跟高斯混合分布 $p(x|\Theta) = \sum_{k}^{}\alpha_{k}\textit{N}(x; \mu_k, \sigma_k)$ 作对比, 发现$\alpha_k$就是$z$的先验分布$p(z=k)$.

$$p(z=k) = \alpha_k$$

而在$z=k$条件下的$x$条件概率就是第$k$个高斯模型.

$$p(x_{i}|z=k,\mu_k, \sigma_k) = \textit{N}(x_i; \mu_k, \sigma_k)$$

现在可以把隐参量代入到对数似然函数中。可以加入冗余项：隐参数在数据$x_i$和高斯参数下的后验概率，从而引入Jensen不等式来简化似然函数。

$$\begin{aligned} L(x|\Theta) &= \sum_{i}\ln\left[p(x_{i}, z|\mu_k, \sigma_k) \right] \\ &= \sum_{i}\ln \sum_{k} p(x_{i}|z=k, \mu_k, \sigma_k)p(z=k) \\ &= \sum_{i}\ln \sum_{k} p(z=k|x_{i},\mu_k, \sigma_k) \frac{p(x_{i}|z=k, \mu_k, \sigma_k)p(z=k)}{p(z=k|x_{i},\mu_k, \sigma_k)} \\ \end{aligned}$$

似然函数简化:

下面通过Jensen不等式简化对数似然函数。

$$f\left[E(x)\right] \geq E\left[f(x)\right]$$

对照Jensen不等式，让$u$指代 $\frac{p(x_{i}|z=k, \mu_k, \sigma_k)p(z=k)}{p(z|x_{i},\mu_k, \sigma_k)}$。

可以得到

$$f(u) = \ln u$$ $$E(u) = \sum_{k} p(z|x_{i},\mu_k, \sigma_k) u$$

得到

$$L(x|\Theta) \geq \sum_{i}\sum_{k} p(z=k|x_{i},\mu_k, \sigma_k) \ln \frac{p(x_{i}|z=k, \mu_k, \sigma_k)p(z=k)}{p(z=k|x_{i},\mu_k, \sigma_k)}$$

于是似然函数简化成对数函数的两重求和。等式右侧给似然函数提供了一个下界。

我们可以根据贝叶斯准则进行推导其中的后验概率

$$\begin{aligned} p(z=k|x_{i},\mu_k, \sigma_k) &= \frac{ p(x_{i}|z=k,\mu_k, \sigma_k)}{ \sum_{k} p(x_{i}|z=k, \mu_k, \sigma_k)} \\ &= \frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\sum_{k}\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)} \end{aligned}$$

定义

$$\omega_{i,k} = p(z=k|x_{i},\mu_k, \sigma_k) = \frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\sum_{k}\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}$$

那么

$$\begin{aligned} L(x|\Theta) &= \sum_{i}\ln \sum_{k} \omega_{i,k} \frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\omega_{i,k}} \\ &\geq \sum_{i} \sum_{k} \omega_{i,k} \ln\frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\omega_{i,k}} \end{aligned}$$

不等式的右侧给似然函数提供了一个下界。EM算法提出迭代逼近的方法，不断提高下界，从而逼近似然函数。每次迭代都以下面这个目标函数作为优化目标：

$$Q(\Theta,\Theta^{t}) = \sum_{i}\sum_{k}\omega_{i,k}^t \ln\frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\omega_{i,k}^t}$$

这个式子表示，在第$t$次迭代后，获得参数$\Theta^t$，然后就可以计算隐参数概率$\omega_{i,k}^t$。 将隐参数代回$Q(\Theta,\Theta^{t})$, 进行最大似然优化，即可求出更优的参数$\Theta^{t+1}$。

迭代求解: 

迭代开始时，算法先初始化一组参数值$\Theta$, 然后间隔地更新$\omega$和$\Theta$。

• 经过$t$轮迭代,已获得一组目标参数$\Theta^t$临时的值。

• 基于当前的参数$\Theta^t$，用高斯混合模型计算隐参数概率 $\omega_{i,k}^t$。然后将隐参数概率代入对数似然函数，得到似然函数数学期望表达式。 这一步叫expectation step.

  $$\omega_{i,k}^t = \frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\sum_{k}\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}$$

• 如前文使用Jensen推导得出，得到每次更新了隐参数$\omega_{i,k}^t$后的目标函数是：

$$Q(\Theta,\Theta^{t}) = \sum_{i}\sum_{k}\omega_{i,k}^t \ln\frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\omega_{i,k}^t}$$

• 利用$\omega_{i,k}$当前值, 最大化目标函数，从而得出新一组GMM参数 $\Theta^{t+1}$. 这一步叫作maximization step。

  $$\Theta^{t+1} = \argmax_{\Theta} \sum_{i}\sum_{k} \ln \omega_{i,k}^t \frac{\alpha_{k}\textit{N}(x_{i}| \mu_k, \sigma_k)}{\omega_{i,k}^t}$$

3.EM算法解单变量GMM

单变量 GMM使用EM算法时，完整的目标函数为

$$Q(\Theta,\Theta^{t}) = \sum_{i}\sum_{k}\omega_{i,k}^t\ln\frac{\alpha_{k}}{\omega_{i,k}^t\sqrt{2\pi\sigma_k^2}}\exp\left[-\frac{(x_i-\mu_k)^2}{2\sigma_k^2}\right]$$

3.1 E-Step:

E-step目标就是计算隐参数的值， 也就是对每一个数据点，分别计算其属于每一种高斯模型的概率。 所以隐参量$\omega$是一个N×K矩阵.

每一次迭代后 $\omega_{i,k}$都可以用最新的高斯参数$(\alpha_k, \mu_k, \sigma_k)$进行更新。

$$\omega_{i,k}^t = \frac{\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \sigma_k^t)}{\sum_{k}\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \sigma_k^t)}$$

E-step 就可以把更新的$\omega$代入似然函数，得到目标函数的最新表达。该目标函数展开如下：

$$Q(\Theta,\Theta^{t}) = \sum_{i}\sum_{k}\omega_{i,k}^t\left(\ln\alpha_k - \ln \omega_{i,k}^t - \ln \sqrt{2\pi\sigma_k^2}-\frac{(x_i-\mu_k)^2}{2\sigma_k^2}\right)$$

3.2 M-Step:

M-step的任务就是最大化目标函数，从而求出高斯参数的估计。 $\Theta := \argmax_{\Theta} Q(\Theta,\Theta^{t})$

更新$\alpha_k:$

在高斯混合模型定义中，$\alpha_k$受限于$\sum_{k}\alpha_k =1$。所以$\alpha_k$的估计是一个受限优化问题。

$$\begin{gathered} \alpha_k^{t+1} := \argmax_{\alpha_k}{ \sum_{i}\sum_{k}\omega_{i,k}^t\ln\alpha_k}\\ \text{subject to} \sum_{k}\alpha_k =1 \end{gathered}$$

这种问题通常用拉格朗日乘子法计算。下面构造拉格朗日乘子：

$$\mathcal{L}(\alpha_k, \lambda) = { \sum_{i}\sum_{k}\omega_{i,k}^t\ln\alpha_k}+ \lambda\left[\sum_{k}\alpha_k -1\right]$$

对拉格朗日方程求极值，也就是对$\alpha_k$求导数为0处，该点就是我们要更新的$\alpha_{k}^{t+1}$值。

$$\begin{aligned} \frac{\partial \mathcal{L}(\alpha_k, \lambda) }{\partial \alpha_k} &= { \sum_{i}\omega_{i,k}^t\frac{1}{\alpha_k}}+ \lambda = 0 \\ \Rightarrow \alpha_k &= -\frac{\sum_{i}\omega_{i,k}^t}{\lambda} \end{aligned}$$

将所有$k$项累加, 就可以求得$\lambda$.

$$\begin{aligned} \sum_{k}\alpha_k &= -\frac{\sum_{i}\sum_{k}\omega_{i,k}^t}{\lambda} \\ \Rightarrow 1 &= -\sum_{i}\frac{1}{\lambda} = -\frac{N}{\lambda} \\ \Rightarrow \lambda &= -N \end{aligned}$$

于是利用地$t$次迭代的隐参量，我们就得到了$\alpha_k$在$t+1$次迭代的更新方程：

$$\alpha_k^{t+1} = \frac{\sum_{i}\omega_{i,k}^t}{N}$$

更新$\mu_k:$ 

$\mu_k$并没有类似$\alpha_k$的限制条件，可以直接把目标函数对$\mu_k$求导数：

$$\mu_k^{t+1} := \argmax_{\mu_k} Q(\Theta,\Theta^{t})$$

让$\frac{\partial Q(\Theta,\Theta^{t})}{\partial \mu_k}=0$, 得到 $\frac{\partial \sum_{i}\sum_{k}\omega_{i,k}^t\left(\ln\alpha_k - \ln \omega_{i,k}^t - \ln \sqrt{2\pi\sigma_k^2}-\frac{(x_i-\mu_k)^2}{2\sigma_k^2}\right)}{\partial \mu_k} = 0$

$$\begin{aligned} \sum_{i}\omega_{i,k}^t\frac{x_i-\mu_k}{\sigma_k^2} = 0\\ \Rightarrow \sum_{i}\omega_{i,k}^t\mu_k = \sum_{i}\omega_{i,k}^tx_i \\ \Rightarrow \mu_k\sum_{i}\omega_{i,k}^t = \sum_{i}\omega_{i,k}^tx_i \end{aligned}$$

所以在$t+1$次迭代， $\mu_k$就用全部$x$的加权平均来求得，权值正是$x_i$属于第$k$个模型产生的概率$\omega_{i,k}^t$。

$$\mu_k^{t+1} = \frac{\sum_{i}\omega_{i,k}^tx_i}{\sum_{i}\omega_{i,k}^t}$$

更新$\sigma_k:$ 

类似地, 将目标函数对$\sigma_k$求极大值：

$$\sigma_k^{t+1} := \argmax_{\sigma_k} Q(\Theta,\Theta^{t})$$

让导数为0：

$$\frac{\partial Q(\Theta,\Theta^{t})}{\partial \sigma_k} = \frac{\partial \sum_{i}\sum_{k}\omega_{i,k}^t\left(\ln\alpha_k - \ln \omega_{i,k}^t - \ln \sqrt{2\pi\sigma_k^2}-\frac{(x_i-\mu_k)^2}{2\sigma_k^2}\right)}{\partial \sigma_k}=0$$

得到

$$\begin{aligned} \sum_{i}\omega_{i,k}\left[-\frac{1}{\sigma_k}+\frac{(x_i-\mu_k)^2}{\sigma_k^3}\right]&= 0\\ \Rightarrow \sum_{i}\omega_{i,k}\sigma_k^2 &= \sum_{i}\omega_{i,k}(x_i-\mu_k)^2 \\ \Rightarrow \sigma_k^2 \sum_{i}\omega_{i,k} &= \sum_{i}\omega_{i,k}(x_i-\mu_k)^2 \\ \end{aligned}$$

高斯模型里面使用的都是$\sigma_k^2$,所以就不需要求平方根了。$\sigma_k^2$的更新方程如下，依赖于更新的$\mu_k$。 所以一般都是先把$\mu_k^{t+1}$算出来，然后再更新$\sigma_k^2$。

$$(\sigma_k^2)^{t+1} = \frac{\sum_{i}\omega_{i,k}(x_i-\mu_k^{t+1})^2 }{\sum_{i}\omega_{i,k}}$$

4.EM算法解多变量GMM

同样的，我们可以得到每次迭代的目标函数如下：

$$Q(\Theta,\Theta^{t}) = \sum_{i}\sum_{k}\omega_{i,k}^t\ln\frac{\alpha_{k}}{\omega_{i,k}^t\sqrt{(2\pi)^d\det(\Sigma_k)}}\exp\left[-\frac{1}{2}(x_i-\mu_k)^T\Sigma_k^{-1}(x_i-\mu_k)\right]$$

其中

• $x_i$是d×1的向量,
• $\alpha_k$ 一个0和1间的值,
• $\mu_k$是d×1的向量,
• $\Sigma_k$是d×d的矩阵,
• $\omega$是N×K的矩阵。

4.1 E-Step:

跟单变量GMM一样，E-step计算隐参数，但是需要用多维高斯分布，利用了多维矩阵乘法和矩阵求逆，计算复杂度要大很多。

$$\omega_{i,k}^t = \frac{\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \Sigma_k^t)}{\sum_{k}\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \Sigma_k^t)}$$

目标函数更新如下：

$$\begin{aligned} &Q(\Theta,\Theta^{t}) \\ &= \sum_{i}\sum_{k}\omega_{i,k}^t\left(\ln\alpha_k - \ln \omega_{i,k}^t - \frac{d}{2}\ln \sqrt{(2\pi)^d} -\frac{1}{2}\ln\det(\Sigma_k)-\frac{1}{2}(x_i-\mu_k)^T\Sigma_k^{-1}(x_i-\mu_k)\right) \end{aligned}$$

4.2 M-Step:

更新$\alpha_{k}:$

多变量GMM下，$\alpha_k$的更新跟单变量 GMM一样。

$$\begin{gathered} \alpha_k^{t+1} := \argmax_{\alpha_k}{ \sum_{i}\sum_{k}\omega_{i,k}^t\ln\alpha_k}\\ \text{subject to} \sum_{k}\alpha_k =1 \end{gathered}$$

得到完全一样的更新方程：

$$\alpha_k^{t+1} = \frac{\sum_{i}\omega_{i,k}^t}{N}$$

更新$\mu_k:$

$$\mu_k^{t+1} := \argmax_{\mu_k} Q(\Theta,\Theta^{t})$$

$Q(\Theta,\Theta^{t})$对$\mu_k$求导，得到

$$\frac{\partial Q(\Theta,\Theta^{t})}{\partial \mu_k} = \sum_{i}\omega_{i,k}^t\frac{\partial \left[-\frac{1}{2}(x_i-\mu_k)^T\Sigma_k^{-1}(x_i-\mu_k)\right]}{\partial \mu_k} = 0\\$$

实数协方差矩阵$\Sigma_{k}$对称的, 其逆矩阵也是对称的。 于是我们可以利用第一部分列出的公式$\frac{\partial (x -s)^TW(x-s)}{\partial x} = -2W(x-s)$求偏导数.

$$\frac{\partial Q(\Theta,\Theta^{t})}{\partial \mu_k} = \sum_{i}\omega_{i,k}^t \Sigma_{k}^{-1}\left(x_i - \mu_k\right) =0$$ $$\Rightarrow \sum_{i}\omega_{i,k}^t x_i= \mu_k\sum_{i}\omega_{i,k}^t$$

所以$\mu_k$的更新方程同样是$x$的加权平均，只是这时候$\mu_k$ is a d×1 向量。 $\mu_k^{t+1} = \frac{\sum_{i}\omega_{i,k}^t x_i}{\sum_{i}\omega_{i,k}^t}$

更新$\Sigma_k:$

$$\Sigma_k^{t+1} := \argmax_{\Sigma_k} Q(\Theta,\Theta^{t})$$

让导数$\frac{\partial Q(\Theta,\Theta^{t})}{\partial \Sigma_k^{-1}} =0$, 得到

$$\begin{aligned} \frac{\partial Q(\Theta,\Theta^{t})}{\partial \Sigma_k^{-1}} &= \sum_{i}\omega_{i,k}^t\frac{\partial \left[ -\frac{1}{2}\ln\det(\Sigma_k)-\frac{1}{2}(x_i-\mu_k)^T\Sigma_k^{-1}(x_i-\mu_k)\right]}{\partial \Sigma_k^{-1}} \\ &= -\frac{1}{2} \sum_{i}\omega_{i,k}^t \left[\frac{\partial \ln\det(\Sigma_k)}{\partial \Sigma_k^{-1}}+\frac{\partial (x_i-\mu_k)^T\Sigma_k^{-1}(x_i-\mu_k)}{\partial \Sigma_k^{-1}} \right] \\ &= 0 \end{aligned}$$

协方差矩阵$\Sigma_k$是对称的,可以利用第一部分的矩阵求导公式 $\frac{\partial \ln \det(X)}{\partial X^{-1}} =-X^T $ and $\frac{\partial a^TXa}{\partial X} = aa^T$，求得极大值$ Q(\Theta,\Theta^{t})$.

$$\frac{\partial Q(\Theta,\Theta^{t})}{\partial \Sigma_k^{-1}} = \frac{1}{2}\sum_{i}\omega_{i,k}^t \left[\Sigma_k - (x_i-\mu_k)(x_i-\mu_k)^T\right] = 0$$

类似地, 我们可以得到$\Sigma_k$在第$t+1$次迭代的更新方程, 它依赖于$\mu_k$。所以我们需要先计算$\mu_k^{t+1}$，然后更新$\Sigma_k$

$$\Sigma_k^{t+1} = \frac{\sum_{i}\omega_{i,k}^t (x_i-\mu_k^{t+1})(x_i-\mu_k^{t+1})^T }{\sum_{i}\omega_{i,k}^t}$$

5.总结

	单变量GMM	多变量GMM
初始化	$$\alpha_{k}^0, \mu_k^0, \sigma_k^0$$	$$\alpha_{k}^0, \mu_k^0, \Sigma_k^0$$
E-Step	$$ \omega_{i,k}^t = \frac{\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \sigma_k^t)}{\sum_{k}\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \sigma_k^t)} $$	$$ \omega_{i,k}^t = \frac{\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \Sigma_k^t)}{\sum_{k}\alpha_{k}^t\textit{N}(x_{i}| \mu_k^t, \Sigma_k^t)} $$
M-Step	$$ \begin{aligned} \alpha_k^{t+1} &= \frac{\sum_{i}\omega_{i,k}^t}{N}\\ \mu_k^{t+1} &= \frac{\sum_{i}\omega_{i,k}^t x_i}{\sum_{i}\omega_{i,k}^t}\\ (\sigma_k^2)^{t+1} &= \frac{\sum_{i}\omega_{i,k}^t(x_i-\mu_k^{t+1})^2 }{\sum_{i}\omega_{i,k}^t} \end{aligned} $$	$$\begin{aligned} \alpha_k^{t+1} &= \frac{\sum_{i}\omega_{i,k}^t}{N}\\ \mu_k^{t+1} &= \frac{\sum_{i}\omega_{i,k}^tx_i}{\sum_{i}\omega_{i,k}^t}\\ \Sigma_k^{t+1} &= \frac{\sum_{i}\omega_{i,k}^t (x_i-\mu_k^{t+1})(x_i-\mu_k^{t+1})^T }{\sum_{i}\omega_{i,k}^t} \end{aligned}$$